티스토리 뷰
Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(1)
미니멀공대생 2024. 9. 12. 23:53Linear Complimentarity problem(선형 상보성 문제)는 강체 간의 접촉을 모델링하는 데 사용하는 방법중 하나다. 이번 글에서는 Linear Complimentarity 을 대수 관점에서 우선 설명하려 한다.
Linear Complimentarity Problem(LCP)
1차원 LCP
LCP의 쉬운 이해를 위해 1차원 문제로 접근해보자. 1차원 LCP에서는 x, y 변수 2개가 있다. 이 둘은 모두 실수에 포함된다. LCP는 상보되는 제약 조건을 만족하는 x와 y를 찾는 문제이다. 이때 제약 조건은 아래와 같다하자.

상보 문제이기 때문에 or가 들어간다. 이를 LCP에서는 아래와 같이 표기한다.

위 문제를 만족하는 해는 단순히 양의 x축과 양의 y축이다.
여기에 y와 x의 선형 관계 y = ax+b를 더하여 해를 찾아보자. 위에서 말한 양의 축과 y=ax+b식과 만나는 점으로 이뤄진 공간이 해가 된다. 이 문제를 수식으로 표현해보면 아래와 같은 형태가 된다.

여기서 y를 ax+b로 변경하여 표현할 수도 있다.
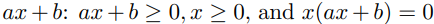
위 식을 이용해 최적화 문제로도 변경할 수 있다.

또 다른 방식으로는 minimum map formulation이다.

min(x,y) 함수는 x<y 라면 x를 반대라면 y를 반환하는 함수이다. 이때 h(x,y)는 0인데, 이는 LCP 문제의 해를 생각해보면 된다. 우리가 가질 수 있는 해는 x>0 라면 y= 0, y>0이라면 x=0으로 2가지 뿐이다. 이 두가지 경우 모두 minimum map 함수는 0을 return하기 때문에 h(x,y) = 0으로 표현할 수 있다.
N차원 LCP
1차원 LCP를 이용해서 n 차원 LCP를 만들 수 있다.
우선 변수들을 선언한다. x, b 는 N차원이 실수에 속하며, A는 실수 NxN 행렬에 속한다. y=Ax+b로 두고 LCP 문제를 표현하면 아래와 같다.

혹은 아래와 같이도 표현할 수 있다.

또한 minimum map formulation을 통해 아래와 같이도 표현할 수 있다.
강체 접촉 모델링을 위한 LCP 표현
강체 접촉 모델링을 위해 우선 구(spheres)끼리의 접촉을 고려하자. n은 시스템에서의 구의 갯수이며, m은 시스템에서의 충돌 갯수이다. 람다_k는 충돌 k에서의 임펄스의 크기이며, 3차원에서 진행한다.
마찰이 없는 접촉 모델
기본적인 물리 상식으로 두 물체가 접촉/충돌 할 때 힘 혹은 임펄스가 작용한다는 걸 안다. 그 반대로 접촉이 아니라면 아무것도 없다는 것도 안다. 이를 이용해서 LCP를 아래와 같이 표현할 수 있다.

d는 두 물체 간의 거리이며, 람다는 두 물체에 적용되는 임펄스의 크기이다. 다만, 거리를 이용하는 건 계산량이 많으니 아래와 같이 거리의 변화율을 이용하자.

이는 결국 두 물체 간의 수직 방향의 상대적인 속도가 0이 아니라면, 둘 사이의 임펄스는 없다 라는 뜻이다. 또한 임펄스가 없다면 두 물체 간의 상대 속도 또한 0이 아니라는 것. 즉, LCP나 두 물체 간의 관통 제약 조건을 강제하고 있다고 볼 수 있다.
다음으로 수직 방향 상대 속도 V_n과 임펄스 간의 선형 관계를 찾아야한다. 임펄스가 작용하고 난 후의 물리 기반 수식을 나타내면 아래와 같다.

v_i는 물체의 초기 속도, v_f는 임펄스 이후의 속도이다. w는 구의 무게이다. 임펄스는 충돌에서의 normal 벡터로 작용한다. 이때 충돌 후의 각 좌표계의 속도는 아래와 같이 표현 될 수 있다.
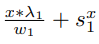
두개의 구의 충돌 이후 속도 벡터를 만들면 아래와 같다.

이를 매트릭스 형태로 식을 표현하면 아래와 같다.

W는 각 좌표계에 맞는 무게다. 이 경우에는 단순히 w1, w2로 이루어진 대각행렬, J는 두개의 구에 작용하는 법선 벡터의 각 좌표 요소이다. 이제 LCP로 표현해보자. LCP 표현을 위해 요소 기반 충돌 후 속도를 충돌에 대한 구 끼리의 상대 속도 식으로 변경해줘야 한다.
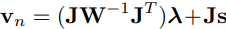
이를 이용해 LCP로 표현하면

마찰이 있는 접촉 모델
마찰 있는 경우의 접촉 모델은 위에서 얘기한 마찰 없는 접촉 모델과 같은 LCP로 표현하지만, 2개의 LCP를 더 추가한 형태이다. 두개의 구 끼리의 하나의 충돌 경우만 고려해보자. 이때 발생하는 법선 임펄스는 람다_n이다. 접촉에서의 마찰 모델을 위해 3차원에서의 polyhedral 뿔을 이용해 선형 근사된 마찰 모델을 사용하자. 마찰 모델이 있으므로 2개의 LCP를 정의해야한다.
t 변수는 polyhedral cone을 정의하는 k 집합의 단위 벡터이다. 람다_t는 마찰에 의한 접선 임펄스다.
추가할 첫번째 LCP는

v_t는 열벡터로 접선 벡터에 의한 충돌 이후의 접선 요소들이다. v_t는 v_n과 같은 방법으로 계산 될 수 있다. 베타는 실수에 속하는 상수이며, e는 1로 이뤄진 열벡터이다. 이 LCP는 마찰이 없는 접촉 모델에서의 관통 방지 LCP와 동일하다.
두번째 LCP는 polyhedral 마찰뿔에 대한 내용이다.

이 LCP는 접선 임펄스가 작용한 polyhedral 뿔의 방향을 정하게 된다. 또한 알파가 0보다 큰 경우에는 접선 벡터 방향의 임펄스가 마찰력과 같아져야 하고 이는 접촉 부분에서의 Sliding을 뜻한다. 반대로 알파가 0이라면 접선 벡터 방향의 임펄스가 마찰뿔 안쪽(정지 마찰력)있게 되면서 접촉 부분이 Sticking이 된다.
위에서 언급 된 3가지의 LCP를 이제 하나로 합치는 작업을 하자. v_n과 v_t는 하나의 벡터로 만들고, 람다도 [람다_n; 람다_t; 베타]로 만들자. 새로운 자코비안도 만들어야 한다. 위에 마찰이 없는 모델에서 만들어진 법선 벡터에 대한 자코비안과 접선 방향을 위한 자코비안과 속도와 람다의 선형 관계를 표현하기 위한 벡터 b를 만든다.

각 방향에 대한 충돌 후 속도 계산을 위한 W와 J의 식을 하나의 행렬로 표현하면 아래와 같다. + 마찰 계수


이렇게 정의 된 행렬들을 이용해 3개의 LCP로 하나의 LCP 형태로 만들어서 표현하면 아래와 같다.

참고 : The Linear Complimentarity Problem and its Applications in Physics Based Animation
Formulating Dynamic Multi-Rigid-Body Contact Problems with Friction as Solvable Linear Complementarity Problems
'미니멀공대생 > Control' 카테고리의 다른 글
| Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(2) :: 접촉 시뮬레이션 (1) | 2024.09.20 |
|---|---|
| contact model, contact force 기초 논문 (0) | 2024.09.19 |
| Homotopy path planning(호모토피 경로 계획) (0) | 2024.09.07 |
| [논문리뷰] Fast Model Predictive Control with Soft Constraints (3) | 2024.08.09 |
| Data Driven Control :: 모델 학습 (Linear, Bayesian, Gaussian Process Regression) (3) | 2024.07.04 |
