티스토리 뷰
Data Driven Control :: 모델 학습 (Linear, Bayesian, Gaussian Process Regression)
미니멀공대생 2024. 7. 4. 17:32Lecture Topic : Linear regression, Gaussian Process Regression, System Identification
최근 학교에서 Data Driven Control 수업들 드디어 들었다. 벌써 까먹기 시작해서 그 전에 조금이나마 정리해두려 한다.
Data Driven을 사용하는 이유는 Non-parametric model을 확인하여 제어 성능을 높이기 위함이다. 주된 방식은 우리가 알고 있는 모델과 실제 로봇의 output 차이를 줄이는 방향으로 최적화를 진행하여 Non-parametric model을 알아낸다. 이번 글에서는 기본적은 Estimation 방식인 Recurisve Least square method부터 Bayesian Linear Regression과 Gaussian Process Regression에 대해서 알아보도록 하자.
Linear Regression

위와 같은 선형 모델을 만들어보자. y_t는 출력, x_t는 입력값이다, W는 파라미터, 엡실론은 노이즈를 나타낸다. LR은 주로 간단한 파라미터를 Estimation 할 때 사용 된다. 로봇으로 예를 들자면 y는 로봇의 상태(로봇의 위치, 속도 등)가 되고 x는 모터 입력(제어 입력)이 된다. 이때 제어 입력과 로봇의 상태의 상관관계를 표현하는 파라미터를 w에 넣게 된다. 즉, 일련의 측정값을 벡터로 모아서 식으로 표현한 형태이다.

실제 값과 예측 값의 차이를 오차로 표현한다. 이 오차의 제곱합을 최소화하는 파라미터 W를 찾는 것이 Least square estimation이 된다. LSE의 경우 데이터를 한번에 모아 파라미터를 업데이트 하게 된다.

다만, 여기서는 행렬의 역이 필요하기 때문에 계산 비용이 높을 수 있다. 이를 해결하기 위해 Recursive Least square를 사용할 수 있다. 역행렬이 없는 RLS를 위해서는 파라미터, 이득 벡터, 오차 공분산 행렬의 업데이트를 순차적으로 반복적으로 진행해줘야한다.


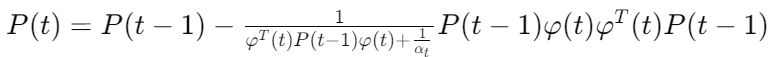
RLS 는 계산에 있어서 이득일 수 있겠지만 초기 파라미터와 공분산 행렬 값이 수렴속도와 추정치에 영향을 줄 수 있다.
Bayesian Linear Regression
베이지안 선형 회귀는 파라미터에 대해 확률적 접근을 한다. 이전 방식들이 모두 결정되어 있었다면, 베이지안을 통해 파라미터들을 확률적으로 접근하여 불확실성을 정량화하고 사전 정보를 모델에 반영할 수 있다. 이를 통해 예측의 신뢰도를 제공한다.
기존 LR과 동일한 형태의 식을 가지지만, 각 값들을 모두 확률적으로 표현해야 한다.
x와 y가 미정의 분포에서 샘플한 i.i.d의 집합이라 하자. LR식에서 노이즈는 독립분포 N(0, sigma^2) 분포를 따르고,

이를 통해 Likelihood를 표현해보자.
입력 데이터인 x와 매개변수 혹은 파라미터 w가 줘어졌을 때, 출력인 y가 나올 확률을 표현하는 likelihood를 나타내면 아래와 같다.

Bayseian Linear Regression에서 파라미터에 대한 분포와 파라미터의 사후는 아래와 같이 표현된다. 여기서 파라미터의 사후라 함은 미래의 파라미터를 예측한다고 생각하면 된다.


파라미터의 미래도 예측했으니, 새로운 입력 x에 대한 출력 y를 예측해보자. Bayseian linear regression에서는 posterior predictive distribution이라 불리는 가능한 출력에 대한 확률적 분포를 말한다.

Bayesian 선형 회귀에서 각 파라미터와 출력등의 분포를 아래와 같이 나타낼 수 있다.

가중치 w의 사후 분포이다.

새로운 포인트 x*에서 출력 y*의 예측 분포이다.
이때 A행렬은 아래와 같은 형태.

베이지안 선형 근사를 하게 되면, 신뢰 구간을 정하여 확인해야 한다. 확률 분포이기 때문이다.
Gaussian Process Regression
Gaussian Process는 연속적인 함수의 집합을 정의하는 확률 모델이다. 유한한 부분집합의 랜덤 변수들이 다변량 가우시안 분포를 따르는 랜덤 변수들의 집합이다. 가우시안을 표현할 때 함수와 공분산은 함수의 형태로 나타내진다.

GP를 적용할 때 유한한 도메인 관점에서 혹은 무한한 도메인 관점에서 볼 수 있다.
유한한 집합 X에 대해서 X를 실수 R에 매핑하는 함수의 집합을 H라 하자. f_o 함수가 H에 속한다 할 때 유한한 X에 대한 실수 값을 벡터 f 값으로 표현할 수 있다.

이런 내용을 이야기 하는 이유는 그저 다수의 함수의 값을 벡터 형식으로 표현할 수 있다는 것을 보이는 것 뿐이다. 이를 통해 함수의 분포를 정의하여 GP 계산을 편하게 해준다.
무한한 도메인은 사실 별게 없다. GP 자체가 무한한 도메인에서 정의 되지만, 위에서 본 것과 같이 유한한 점 집합에 대해서는 다변량 가우시안 분포를 가진다는 특징이 있다. GP는 f: X-> R를 모델링하는데, 이때의 함수 f가 무한할 수 있다. 실제 로봇 시스템에서 무한한 도메인 같은 느낌은 없고, 모두 유한한 형태를 가지게 된다.

결국 뭐가 됐든 유한한 다변량 가우시안 분포가 된다는 사실이 전부.
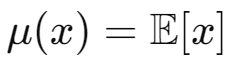
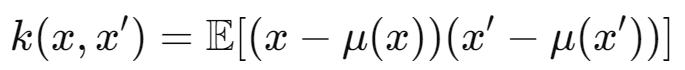
유한하던, 무한하던 위 내용이 시사하는 바는 어떤 함수들에 대한 확률 분포를 모델링하는 데 사용될 수 있다는 점이다. mean에 따라 혹은 다양한 공분산 함수(혹은 두 데이터 간의 관계를 말하는 "커널"이라고 이야기할 수도 있다.) 를 통해 상관 관계들을 표현할 수 있다. 커널 종류로는 Linear Kernel, Polynomial Kernel, Rational Quadratic Kernel,Matern Kernel 등이 있다.
이번 글 제목을 모델 학습이라 한 이유는 GP에서도 Training set과 testing set이 있기 때문이다. 우리가 모르는 분포 S에서 나온 testing point들은 같은 분포에서 나온 Training set으로 학습 된 GP를 통해서 예측 될 수 있다.
GP는 기본적으로 Training에서의 X값과 testing에서의 X_* 입력에 대해 함수 f가 다변량 정규 분포를 따른다고 가정한다. 이 때 zero-mean GP라 하면 가우시안 분포는 아래와 같이 표현된다. 노이즈 또한 비슷한 모양으로 표현될 수 있다.
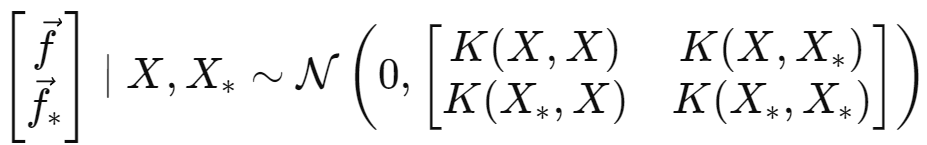
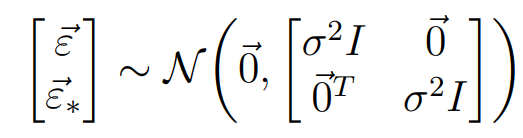
최종적으로 독랍 가우시안 랜덤 변수의 합 또한 가우시안이기 때문에 아래와 같이 식을 정리할 수 있다.

이 가우시안의 평균과 공분산의 경우 아래와 같이 표현될 수 있다.

'미니멀공대생 > Control' 카테고리의 다른 글
| Homotopy path planning(호모토피 경로 계획) (0) | 2024.09.07 |
|---|---|
| [논문리뷰] Fast Model Predictive Control with Soft Constraints (3) | 2024.08.09 |
| [MCube-MIT] Manipulation 연구 정리 (0) | 2024.04.15 |
| [논문리뷰] In-Hand Manipulation via Motion Cones (1) | 2024.03.22 |
| [논문리뷰] Prehensile Pushing : In-hand Manipulation with Push-Primitives (1) | 2024.03.14 |
