티스토리 뷰
어떤 시작점과 도착점으로 이뤄진 두 경로가 동일한 공간 안에서 장애물을 넘지 않고 서로 변형될 수 있다면 두 경로는 호모토피 클래스에 속한다고 한다.
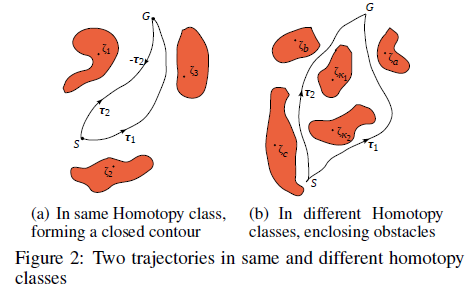
figure2의 왼쪽의 경로들은 같은 호모토피 클래스이고 오른쪽은 중간에 장애물로 인해 다른 호모토피 클래스가 된다.
호모토피 경로 계획 문제는 시작점에서 도착점으로 가는 여러 경로들 중에 위상적으로 구별되는(즉, 다른 호모토피 클래스에 속하는) 최적 경로를 찾는 문제이다. 일반적인 경로 계획과는 다르게 장애물의 오른쪽으로 가야할지, 왼쪽으로 가야할 지를 고려한다고 보면 된다.
주로 장애물 기준으로 시계 방향이냐, 반시계 방향이냐에 따라 서로 다른 호모토피 클래스가 나뉜다. 이런 다른 호모토피 클래스 중에 최적 경로를 찾는 게 목표이다.
최적 경로란 길이의 최적일 수도, 시간의 최적일 수도 혹은 에너지 효율과 같은 것들이 최적일 수도 있다.
주로 모바일 로봇에서 많이 고려된다고 볼 수 있지만, 일반적으로 장애물 사이를 이동해야 하는 문제들의 경우에 전부 사용 될 수 있다. 로봇 팔 같은 경우도 특정 물체를 조작한다고 했을 때 장애물 사이에서 어떤식으로 라우팅을 하는 게 좋은지에 대해 고민할 때 사용되는 플래닝이다.

경로들을 찾아야하기 때문에 우리가 일반적으로 알고 있는 경로 플래닝 알고리즘들 기반으로 두고 진행한다. 다만, 기본 탐색 기반 플래닝 알고리즘으로는 클래스간 경로를 비교하는 것만 가능하고 효율적으로 경로 탐색을 하지는 못한다. 호모토피 클래스를 효율적으로 표현하는 방법들이 있고(내가 읽은 논문에서는 Cauchy 적분 정리와 복소 해석학 이용) 이를 그래프 탐색 기반의 최적 경로 계획에 통합하여 진행한다.
참고 : Search-based Path Planning with Homotopy Class Constraints
Homotopic Path Set Planning for Robot Manipulation and Navigation
'미니멀공대생 > Control' 카테고리의 다른 글
| contact model, contact force 기초 논문 (0) | 2024.09.19 |
|---|---|
| Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(1) (2) | 2024.09.12 |
| [논문리뷰] Fast Model Predictive Control with Soft Constraints (3) | 2024.08.09 |
| Data Driven Control :: 모델 학습 (Linear, Bayesian, Gaussian Process Regression) (3) | 2024.07.04 |
| [MCube-MIT] Manipulation 연구 정리 (0) | 2024.04.15 |
