티스토리 뷰
Fast Model Predictive Control with Soft Constraints
저자 : Arthur Richards
논문 : https://www.sciencedirect.com/science/article/pii/S0947358015000667
작성 : 이해구
Wang and Boyd의 Fast MPC방식에서 발전한 방법이다.(https://pasus.tistory.com/230 참고)
이들은 소프트 제약조건을 추가하는 효율적인 방법에 대해서 다뤘다. 다양한 robust mpc 방식들은 모델 불확실성은 어느정도 가져간 상태에서 robust함을 가지고 꽤 복잡한 형태이다. 이보다 쉬운 방법은 제약 조건을 어느정도 어기도록 최적제어기를 설계하는 것이다. 이를 위해서는 주로 여분의 변수 (slack variables)를 사용하여 제약조건 위반의 등급을 표현한다.
논문에서는 여분의 변수를 사용하지 않고 목적 함수에 직접적으로 제약조건의 위반을 적용하는 방법에 대해 다룬다.
중요하게 알아야하는 부분은 온라인으로 풀려야 하는 QP의 Hessian matrix의 sparsity pattern을 유지해야 한다는 점이다. (convex라는 뜻일듯?) W&B 논문에서는 고도로 조작된 (tailored) Hessian의 factorization을 통해 Newton step을 매우 효율적으로 계산하는데, 논문에서는 소프트 제약 조건을 결정 변수 (decision variables)을 추가한다거나 hessian의 구조를 바꾸는 것 없이 적용할 수 있는 방법을 소개한다.
소프트 제약 조건 위반은 nonsmooth 함수일 때 가장 사용하기 좋다. nonsmooth 목적 함수는 빠른 그라디언트 기반 최적화에서 문제가 될 수 있기 때문에 Kreisselmeier-Steinhauser (KS) 함수를 사용하여 위반을 부드럽게 근사해준다. 1-norm 패널티 근사는 "명확한 패널티 함수" 보증을 잃어버리게 된다. 다만 이를 잃으면서 비연속적인 부분에서도 최적화가 가능하게 해준다.
논문에서도 KS함수를 이용하여 소프트 위반 제약 조건을 적용한다. KS함수는 logarithmic barrier function이 강한 제약 조건을 근사하는 것처럼 소프트 제약 조건을 근사한다.
Forming and Solving the QP
일반적인 선형 다이나믹스. 제약조건과 Quadratic cost를 가진 mpc를 먼저 보고가자.

결정변수 (decision variable)은 u(k~k+N-1)과 x(k+1 ~ k+N)이다. 변수들을 정리하여 하나의 벡터 z로 모으면 아래와 같이 표현할 수 있다.

이런 작업은 mpc에서 자주 보이는 매트릭스 변환인데, Banded structure(대각행렬 형태) 형태로 만들어 계산을 빠르게 하는 것이다. 여기에 W&B는 로그 배리어 함수를 inequality 제약조건으로 사용했다.

여기서 p_i벡터는 P 행렬의 행이 된다. 이런 형태의 로그 배리어 함수를 목적 함수에 넣어 최적화 문제를 eqaulity만 있는 형태로 변경하여 eqaulity-constratined nonlinear program을 만든다. 중요한점은 이런식으로 변경하여도 convex는 유지되어 Newton method 같은걸로 최적화를 풀 수 있다.

Newton 방식으로 풀기 위해 잔차(residual)를 계산할 때 라그랑주 상수를 추가하여 식을 정리해보면 아래와 같다.

최적해 수렴 조건은 잔차들이 모두 0이 되는 것이다. 이를 위해 z와 라그랑주 상수에 대한 선형 시스템을 아래와 같이 표현할 수 있다.

이때 파이는 뉴턴스텝으로 헤시안 행렬과 로그 배리어 함수로 이루어진 형태이다.

여기서 Fast MPC의 중요한점은 파이와 c 행렬이 희소 구조(Sparse)를 가진다는 점이다. 이를 통해 선형 시스템을 매우 효율적으로 풀 수 있게 된다. 자세한 내용은 ("Fast model predictive control using online optimization") 참고.
Including soft constraints
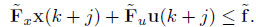
소프트 제약을 추가하는 방법에 대해 알아보자. 상태변수와 제어입력에 대한 제약조건을 ~F로 표현한 상태이다. ~f는 각 제약 조건의 최대 허용치를 표현한다. 제약을 만족하지 못할 경우에 대한 위반 정도를 아래와 같이 표현한다. 이를 목적함수에 norm 형태로 추가하면 된다.

소프트 제약을 가장 쉽게 적용하는 방법은 모조 제어 입력(dummy)을 넣어 여분의 변수(slack variable)처럼 작동하게 하는 거다. 이를 s라 표현하고 정리하면 아래와 같이 소프트 제약이 하드 제약 조건 포맷으로 변경됨을 볼 수 있다.

모조 제어 입력 s는 0이상이며 기존 제약 조건인 fx+fu-f보다 커야하는 형태이다. 이는 위 mpc의 목적함수에서 u에 대한 가중치를 변경하면 ([0T, 1] 형태로) 동일하게 가져갈 수 있다. 즉 모저 제어입력 형태로 소프트 제약조건을 넣는 것은 단순히 MPC 형태에서 바로 적용가능하다는 뜻이다.
(이 부분이 살짝 어려울 수 있는데, 잘 곱씹어보자) 단, 앞서 말했듯이 이 방법을 하기 위해서는 추가적인 결정 변수를 사용해야 한다. 따라서 논문에서는 이를 해결한 방법을 제안한다.
The Kreisselmeier-Steinhauser function
KS 함수는 함수 집합의 최대값을 매끄럽게 근사해준다. (Systematic control design by optimizing a vector performance index)

g(x)가 여러 제약 조건들이 될 수 있고, 로우는 최대값에 얼마나 가깝게 근사할지 조절해준다. 로우가 커질 수록 KS 함수는 g(x) 함수의 최대값에 가깝게 근사된다. 물론 너무 크면 exp하게 증가하여 문제가 될 수 있다. 이를 해결하기 위해 아래와 같은 형태로 변경하여 사용한다.


위 figure는 두개의 선형 함수에 대한 최대 근사를 보여준다. KS 함수가 로그 배리어 함수의 효과랑 동일하게 불연속 구간에서 부드럽게 근사하는 걸 확인할 수 있다.
논문에서는 이 KS 함수를 이용하여 최대 제약 위반 정도 V 함수를 부드러운 표현하려 한다. 앞서 말한 제약 조건 식을 아래와 같이 정리하자.

이때 위반 항을 아래와 같이 표기된다.

KS 함수를 최대 operator에 적용하면 아래와 같은 매끄러운 위반 함수가 만들어진다.

Fast MPC Newton 방식에 적용하기 위해 gradient와 hessian을 구해야 한다. KS 함수를 사용할 때 큰 지수 함수가 발생할 수 있기 때문에 앞서 말한 형태와 유사하게 최대값을 offseting 하는 형태로 진행한다. 이는 2개의 지수함수를 정의하는 형태로 진행된다. 하나는 제약 조건이 성립할 때 하나는 위반될 때.
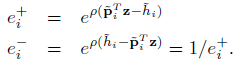
이때 위반 함수의 경사는 아래와 같이 표현된다.
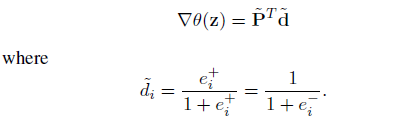
또한 위반 함수의 Hessian은 아래와 같다.

이를 이용해 Newton step을 위한 시스템 식을 아래와 같이 변경할 수 있다.
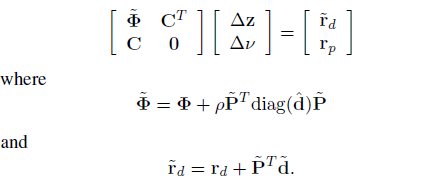
논문에서는 간단한 시뮬레이션으로 여분의 변수와 KS 함수를 사용하는 것을 비교한다. 시뮬레이션엔 일정한 외란이 모델링 되지 않은 채 mpc에 들어가고 이로인해 제약조건 위반이 일어나게 된다.
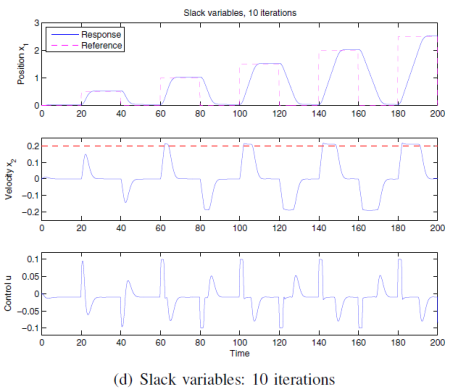

slack variable을 사용할 경우 10번의 반복 후에 reference를 따라가는 반면 KS 함수를 사용하면 4번만에 reference를 따라가는 모습을 볼 수 있다.
논문에서는 선형 모델을 사용했기에 비선형 모델에 대한 내용은 검증이 필요할 것 같다. 또한 실제로 적은 횟수의 iteration은 KS가 계산이 빨랐지만 KS 함수가 지수함수로 늘어나는 문제로 인해 반복 횟수가 높아지면 계산 시간이 오래걸리고 이로 인해 Slack variable을 사용하는 것보다 더 오래 걸릴 수도 있을 것 같다.
'미니멀공대생 > Control' 카테고리의 다른 글
| Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(1) (2) | 2024.09.12 |
|---|---|
| Homotopy path planning(호모토피 경로 계획) (0) | 2024.09.07 |
| Data Driven Control :: 모델 학습 (Linear, Bayesian, Gaussian Process Regression) (3) | 2024.07.04 |
| [MCube-MIT] Manipulation 연구 정리 (0) | 2024.04.15 |
| [논문리뷰] In-Hand Manipulation via Motion Cones (1) | 2024.03.22 |
