티스토리 뷰
In-Hand Manipulation via Motion Cones
저자 : Nikhil Chavan-Dafle, Rachel Holladay, and Alberto Rodriguez
논문 : https://arxiv.org/abs/1810.00219
작성 : 이해구
Intro
모션 콘은 마찰이 있는 밀림 동작에서 강체가 가질 수 있는 모션의 집합이다. 마찰 접촉에 대한 underactuated 시스템이라고 볼 수 있겠다. Horizontal pushing task에서 point contact일 때 line contact 일때에 대한 연구에서 발전됐고, 효율적인 경로 계획, 제어의 기초로 사용됐다.
논문에서는 평면에서의 테스크들을 조금 더 일반화시켜 모션 콘을 만드는 방법에 대해 보여준다. 수직 평면에서의 prehensile manipulation을 좀 더 집중해서 다룬다. 밀림 동작만이 아닌 외력에 의한 동적인 반응도 모션콘으로 확인하여 테스크를 더 잘 수행할 수 있게 된다.
- Mechanics : 중력방향에서의 평면에 대한 모션 콘을 보여준다.
- Experimental : 모션 콘의 Stick/Slip 조건에 대해 실험적 검증을 한다. (Vicon 모션 트래커 사용)
- Application : 간단한 prehensile push 동작에 샘플 기반 플래닝 프레임워크에서 모션 콘을 사용한다.

위 사진에서 보이는 게 모션콘으로 이뤄진 pushing 전략 경록이다. friction cone과 동일하게 motion cone 평면에 있을 경우 물체가 slide하게 되는데, 이를 사용하여 물체를 어떻게 push하여 원하는 모양을 얻을지 플래닝할 수 있다. local reachability를 motion cone으로 확인할 수 있다. 논문에서는 플래닝을 계획하는 데 1초 미만으로 걸린다고 한다.
Related work
Goyal은 limit surface(Planar sliding of a rigid body with dry friction: Limit surfaces and dynamics of motion, 1989)라는 개념을 정의한다. limit surface는 slider와 지면과 접촉에서의 sliding twist 간의 간단한 매핑이다. 그리고 Mason(Mechanics and Planning of Manipulator Pushing Operations, 1986)이 motion cone이라는 개념을 정의한다. 이 두개의 근본적인 기하학적 구축이 접촉 작용에 대한 힘-모션 매핑을 제공한다. 또한 이를 통해 non-prehensile manipulation에서 효율적인 플래닝과 제어를 할 수 있게 해준다.

기존 Motion cone의 경우 (a) 환경에서만 가능했는데 논문은 b,c,d 모두 가능하도록 확장시켰다.
Limit surface
제약 평면은 물체와 지탱해주는 접촉의 마찰 상호작용을 모델링하는 데 사용된다. 위 사진에서 a와 b에서 물체가 놓여져 있는 평면이 지탱 접촉이다. c와 b에서는 손가락 접촉이 같은 작용을 한다. 몇 논문에서는 limit surface의 타원형 근사를 사용한다.
w = [fx, fz, my]로 두고 이를 접촉 프레임에서 지탱 접촉으로 부터 물체에 전달되는 마찰 렌치라고 하자. 타원형 제약 평면을 수학적으로 표현해보면 아래와 같다.
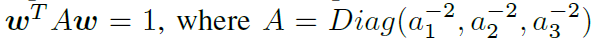
등방성(isotropic) 마찰에 대해서는 최대 마찰 힘이 a1 = a2 = mu_c*N이 된다. 접촉 수직에 대한 최대 마찰 토크는 a3 = r_c*mu*N인데 r은 접촉의 반경이 된다. c는 적분 상수인데 일정한 압력의 분포의 경우 0.6이 일반적이다.
물체가 지탱 접촉에서 미끄러질 때, 접촉과 물체 사이의 마찰 렌치는 접촉 평면을 교차하게 된다. 최대 에너지 산일 원리(maximal energy dissipation)에 의해서 교차점에서의 제약 면에 대한 수직은 접촉에서 물체의 twist의 방향을 알려준다.
반대로 물체의 twist를 알면, friction wrench를 알 수 있기도 하다.

v_obj_c는 접촉 프레임에서의 물체의 속도이고, 이는 Jc = 물체 프레임에서 접촉 프레임으로의 매핑 행렬로 계산 될 수 있다.
타원 제약 평면 모델 가정으로 접촉 프레임에서의 물체의 직선 속도는 선형 마찰과 항상 반대이다. 또한 마찰 렌치와 접촉 평면 수직과의 관계는 선속도와 각속도의 제약조건을 아래처럼 만든다.

지탱 접촉으로부터 생기
는 물체의 마찰 렌지로 물체 속도를 계산할 수 있게 된다.
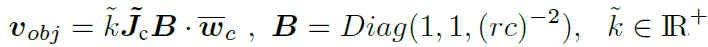
~J_c의 경우 지탱 접촉 프레임으로부터 물체 속도를 물체 프레임으로 매핑해준다.
- Generalized friction cone
물체 프레임에서의 접촉에 대한 지역 마찰 콘을 Generalized friction cone이라 한다.

J_p의 경우 pusher의 지역 접촉 힘(f_p)을 물체 프레임으로 매핑해준다. -w는 pusher의 일정한 접촉으로 생기는 마찰 콘안에 있는 단위 힘 -fp에 반응하는 단위 렌치이다.
이를 통해 이제 역학적 접근을 고민해보자.
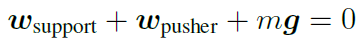
물체 프레임에서 식을 전개해보자. support는 지탱 접촉이 만드는 마찰 렌치, pusher는 푸셔가 만드는 렌치, mg는 중력에 의한 렌치가 된다. 프레임 변환을 통해 물체 프레임들로 전부 바꿔줘야한다.
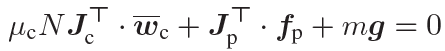
- Stable pushing in a plane
Pusher가 물체와 접촉해서 힘을 가하면 이를 stable pushing 이라 한다. 이를 위해서는 pusher의 힘이 지역 접촉 프레임에서의 마찰 콘 안에 있어야 한다.

이 식을 다시 정리하면

즉, 접촉 마찰 렌치와 중력으로 인한 렌치를 pusher 렌치가 맞출 수 있어야 한다.
stable push로 모션이 만들어질 수 있는지 확인 하려면, 필요한 net 렌치가 pusher의 generalized friction cone 안에 들어가는 지 보면 된다.

제어 관점에서 미는 동작이 안정적인지 보는 것보다는 특정 미는 동작이 원하는 방향이나 위치로 이동시킬 수 있는지와 예측 가능하고 일관적인지를 보는 게 중요하다. 따라서 stable push가 필요한 것이다.
Motion cone for planar pushing
gfc 안에 있는 pusher에 의한 wrench로 필요한 net wrench가 안정되는 경우에서 물체의 모션 집합을 찾는 것이 문제이다. 이는 stable push 조건을 만족하는 경우이므로 정리하면

이모션 콘을 찾기 위해서는 위 조건을 만족하는 지탱 접촉 렌치를 찾고 이들의 집합을 물체의 twist에 매핑해야 한다. 물체의 twist 집합(모션 콘)을 ~V_obj으로 나타낸다.
우선 문제는 쉽게 하기 위해 중력이 없는 horizontal surface에서의 pushing을 생각해보자.
Motion cone for pushing on the horizontal surface
땡갓 중력 = 0
물체가 평면에 일정한 압력 분포로 올라 있을 때 접촉 프레임은 물체 프레임과 동일 하다. 따라서 J_c ,~J_c는 단위 행렬이 된다. 위에서 말한 식을 정리하면

가능한 지탱 접촉 렌치의 집합은 pusher의 generalized friction cone의 반대이다. (negative) ~W_c를 통해 모션 콘 ~V_obj을 얻을 수 있다. ~W_c와 ~V_obj은 convex polyhedral cone들이고 지탱 수직 힘에 독립적이다. 즉, 물체의 무게 중력과 마찰 평면 마찰계수와 독립이라는 뜻. 이 말은 결국 물체의 무게나 마찰계수와 상관 없이 물체의 움직임은 마찰 콘으로 표현될 수 있다는 것이다.
위에 식을 살펴보면 중력이 물체에 만드는 렌치가 필요한 net 렌치를 푸셔의 generalized 마찰 콘 안/밖으로 옮기는 걸 볼 수 있다. 즉 중력 힘에 때문에 어떤 평면과 중력 방향에 따라 stable push일 수도 아닐 수도 있다는 뜻이다.
가정 1 : 중력이 없는 모션 콘안에서의 모든 밀기 동작들은 특정 임계값 이상의 집는 힘을 준다면 중력 평면에서도 안정적인 밀기가 될 수 있다.
증명 : 중력이 없는 모션 콘 안에서의 모션에서는 지지/집는 렌치 방향이 pusher의 gfc 안에 있다. 수식으로 표기하면


net 렌치가 pusher의 gfc안 쪽에 있도록 지지/집기 렌치 방향으로 얼만큼 커져야 하는지를 정하는 mu_c*N를 찾을 수 있다. 주어진 mu_c로 analytically하게 gfc안쪽에 넣을 수 있는 N의 범위를 찾을 수 있다. 사진에서처럼 N을 키워 Net wrench를 cone 안쪽에 넣을 수 있다. 이론적으로는 가능하지만, 그리퍼의 집기 힘은 한정되어 있기 때문에 한정된 상황에서 motion cone 안쪽에 넣을 방법을 찾아야 한다.
Motion cone in the gravity plane for fixed grasping force and friction parameters
정해진 그리퍼 힘과 마찰 파라미터로 중력 있는 상태에서의 모션 콘을 찾는 경우를 생각해보자.
Analytical Computation
Stable Pusher 렌치 안에 있는 pusher 렌치를 알 때,

위 식은 3개의 선형 eqaulities 집합과 4개의 미지수가 있다. 4개의 미지수는 k와 w_c이다. 하지만 contact 렌치인 w_c의 단위 벡터가 타원형 제약 평면 조건을 만족한다는 걸 안다.

따라서 위 식 2개는 analytical하게 같이 풀 수 있으며, 이를 통해 k와 w_c를 찾을 수 있다.
9번식을 타원형 식에 넣어서 정리하면, 위 식은 k에 대한 2차 식으로 바뀐다. k가 positive real numer라는 조건을 이용해 2차식을 풀면 해를 구할 수 있다. 이를 이용해 9번식을 정리하면 3개의 미지수와 3개의 선형 equlities 조건으로 만들고 이제 단일 해를 구할 수 있다.
중력 평면에서는 ~W_c와 W_pusher의 관계가 선형은 아니다. ~W_c 집합을 찾기 위해서 -w_pusher를 W_pusher의 경계로 나가서 9번과 그 밑에 식을 반복적으로 풀어야 한다.

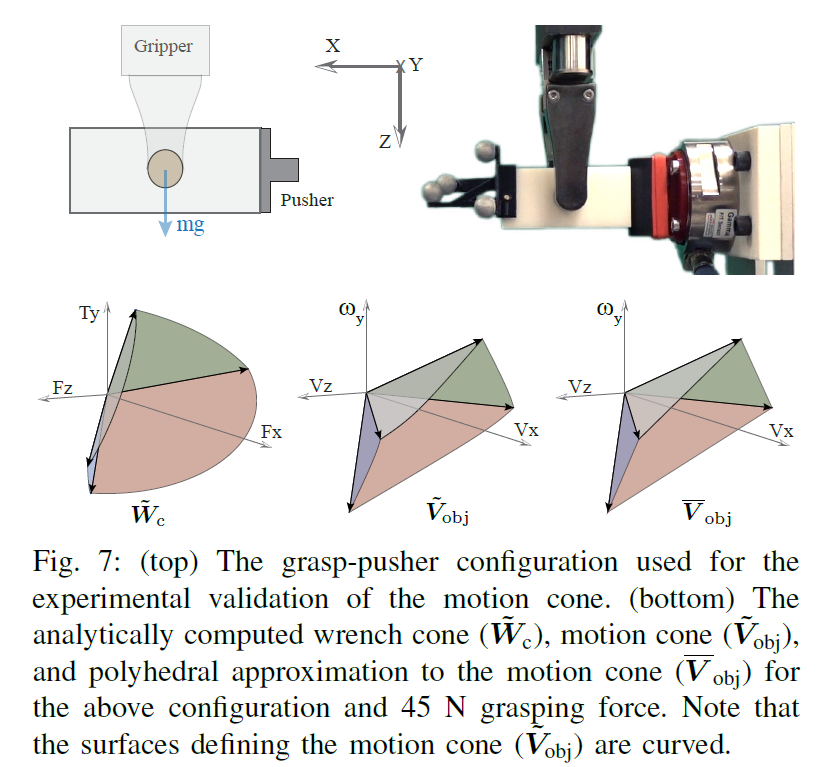
위 그림은 ~W_c를 계산하기 위한 방법을 보여주고 있다. pusher의 gfc와 중력에 의한 렌치의 합과 제한 평면과의 교집합이 렌치 집합이 되는 형태이다.

위 사진은 ~J_c를 이용해 계산 된 wrench 집합을 motion cone ~V_obj로 바꿔주는 모습을 표현한다.
Polyhedral Approximation to the Motion cone
물체가 그리퍼 사이에서 밀릴 때, 물체 프레임 기준으로 그리퍼 손가락 접촉 위치는 변한다. 따라서 G_c와 모션 콘 또한 변하게 된다. 따라서 물체가 움직임에 따라 모션 콘을 계속 적으로 계산 해줘야 한다.
-V_obj으로 polyhedral approximation 모션 콘을 제안한다. 각 엣지는 모션과 연관이 있다.
정리하자면
- W_pusher의 엣지에 대한 w_c와 w_pusher를 계산한다
- 1번에세 계산 된 w_c의 집합을 이용해서 wrench cone -W_c를 정의한다.
- -W_c를 V_obj 모션콘을 얻기 위해 물체 twist space로 매핑한다.
Motion cone을 정의함에 따라 도달 가능한 공간? 부피를 알 수 있고, 이를 이용해 플래닝을 하여 더욱 빠르게 진행 할 수 있다. 쉽게 말해 search space를 많이 제약해주는 느낌.
논문이 조금 복잡하다. 쉬운 것 같으면서도 구현하려고 하면 디테일한 부분들의 설명이 조금 부족하거나, 아직 모르는 것들이 많아서 어렵다. 이전에 리뷰한 push primitive 는 전부 구현했는데 이제 motion cone을 한번 구현해봐야겠다..과연..
'미니멀공대생 > Control' 카테고리의 다른 글
| Data Driven Control :: 모델 학습 (Linear, Bayesian, Gaussian Process Regression) (3) | 2024.07.04 |
|---|---|
| [MCube-MIT] Manipulation 연구 정리 (0) | 2024.04.15 |
| [논문리뷰] Prehensile Pushing : In-hand Manipulation with Push-Primitives (1) | 2024.03.14 |
| Integral Adaptive Law와 Persistent Excitation에 관하여 (2) | 2024.03.08 |
| [논문리뷰] Control Barrier Functions : Theory and Applications (1) | 2024.01.03 |
