티스토리 뷰
Controal Barrier Functions : Theory and Applications
저자 : Aaron D. Ames1 , Samuel Coogan2 , Magnus Egerstedt3 , Gennaro Notomista4 , Koushil Sreenath5 , and Paulo Tabuada
논문 : https://arxiv.org/pdf/1903.11199.pdf
작성 : 이해구
safety-critical system이라는 용어는 안전성을 메인 디자인 기준으로 두는 시스템을 말한다. 그렇다면 안전성이란 정확히 뭘까? bad 행동은 일어나지 않고 good 행동은 "결국" 일어나야 하는 것이 safe라면, asymptotically stable은 equilibrium point에 결국 도달하기 때문에 safe하다고 할 수 있다. 동일하게 invariance(불변) 또한 safe의 속성으로 볼 수 있다. 경로 자체가 불변 set에서 시작되면 복소평면의 여집합으로 가지 않기 때문에이다.
본 논문의 목적은 control barrier functions을 소개하면서 안전성에 대한 논의를 새롭게 해보자이다. liveness 속성에의 lyapunov function의 역할처럼, CBFs 또한 안전성에서 동일한 역할을 하게 된다.
- Lyapunov 함수: 주로 시스템의 안정성을 분석하는 데 사용된다. Lyapunov 함수는 시스템의 상태를 나타내는 함수로, 시스템이 어떤 초기 조건에서 시작하더라도 이 함수 값이 시간이 지남에 따라 감소하면 해당 초기 조건에서의 안정성이 보장된다.
- Control Barrier Functions (CBFs): 주로 안전성을 보장하고자 하는 물리적 시스템에서 사용된다다. CBFs는 시스템이 안전한 상태로 향하도록 보장한다. 즉, 시스템이 미리 정의된 안전 영역 안에 남아 있도록 하는데 사용된다.
최근 연구에서 CBFs가 대두 되는 이유는 자율 시스템에 대한 관심이 높아졌기 때문이다.기본적으로 자율 시스템은 미지의 비정형적인 환경에서 움직이기 때문에 안전 속성들을 설정하기가 어렵기 때문이다. 또한 최신 CBFs들은 리아프노프와 리아프노프 함수 기반 제어 디자인들이 안전 고려 사항을 다루기 위해 적절하게 전이될 수 있다는 것을 시사한다.
History of Barrier Functions
주어진 다아니믹 시스템에서 x가 n차원의 실수에 속할 때, safe set C가 smooth function h (연속인 함수, n차원을 1차원 실수로 매핑하는 함수)의 superlevel set이라고 가정하자. 이때 h(x)가 0보다 크거나 같게 만드는 x의 집합을 superlevel set이라 하고 이게 safe set C가 된다는 뜻이다. 단, x에 대한 h 함수의 편미분 값이 0이 아니어야 한다.
그러면 Nagumo 이론은 C의 바운더리에서의 h의 미분에 대한 값을 기준으로 불변 set을 위한 필요충분 조건을 주어준다.
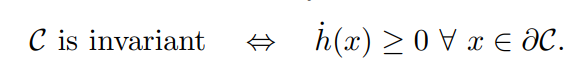
barrier certificates(베리어 증명서)의 경우 시스템이 안전한 상태로 수렴하도록 보장하기 위한 수학적 도구이다. unsafe set과 시스템이 시작하는 초기 조건 set이 있다고 하자. 이때 B라는 시스템의 상태를 나태내는 함수 barrier certificate가 있다. 입력이 초기 조건 set에 있을 경우 0보다 작아야하고, unsafe set일 경우 0보다 커야 한다. 결국 B는 아래 조건을 만족할 경우에 베리어 증명서가 된다.

unsafe set의 여집합을 safe set으로 고르고, B(x)를 -h(x)로 할 경우 베리어 증명 조건은 h의 미분값이 0보다 크게 되고 이는 결국 C가 불변이라는 게 된다.
기존 리아프노프 기법들은 집합의 바운더리에서만 안전성을 판단했는데, 리아프노프-같은 방법들은 집합 전체를 고려하려는 시도라고 한다. 경계를 넘어서도 안전성을 유지하여 안전한 시스템을 보장하려 한다는 뜻.
예시로 barrier lyapunov function를 보여준다. 리아푸노프 함수와 유사한 역할을 수행하지만, 모든 측면에서 positive definite해야 한다. B의 미분값이 0보다 작게 하여 집합 C의 불변성과 안전성을 보장하게 된다. 이로 인해 안전성도 보장되며 집합 C의 경계를 너머 안전성을 확장할 수 있게 된다.
다만, 모든 레벨에서의 불변성을 강제할 수 있다는 게 단점이다. 불필요하고, 유연하지 않으며, 계산 및 성능 저하 등에 단점이 야기 된다.
위에서 언급한 시스템의 경우 closed dynamical system들이지만, viability에 대한 연구는 open dynamical system으로 확장시켰다. 여기서는 불변 set들을 제어 가능한 불변 set으로 옮기는 게 필요하고, 이는 컨트롤러를 알맞게 디자인함으로서 얻을 수 있다.
barrier certificate(BC)은 control barrier function(CBF)으로 확장됐는데, BC의 경우에는 시스템만 고려했다면 CBF의 경우 컨트롤러가 시스템이 미치는 영향까지 고려하게 됐다. 주어진 컨트롤 시스템 및 함수 h에 의한 정의된 안전한 set C에 대해서의 조건은 아래와 같다.
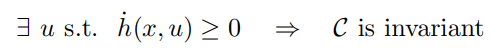
논문에서는 control lyapunov barrier functions라는 것도 안전성과 안정성을 동시에 보장하기 위해 만들어졌다고 한다. 단, 이런 경우 최종적으로 h함수의 미분이 0보다 크거나 동일하다는 조건으로 강제화 되어 축소된다. 이런 조건은 우리가 필요한 것보다 더 과하기 때문에(강요) CBF에 대한 연구가 현재 이뤄지는 형태이다.
CBFs의 경우에는 barrier function 조건을 안전한 집합 전체로 확장하기 위한 것임을 알아두는 게 중요하다. 이는 아래와 같이 정의된다.

알파에 대한 조건이 필충조건이며, 최소한의 제한만 한다. 따라서 조건이 모든 set C로 바뀌면서 안전한 컨트롤러를 합성하는 방법을 제공하게 된다. 즉, 최적화 기반 제어 방식을 사용하면서 최소한의로 제어기를 수정하여 safety critical control를 제공하게 된다.
FOUNDATIONS OF CONTROL BARRIER FUNCTIONS
control Lyapunov functions(CLFs)
아래와 같은 비선형 affine 시스템이 있다고 하자.

f 와 g는 지역적으로 Lipschitz 함수임을 전제한다. Lipschitz 함수란 정의 된 공간에서 특정한 제약 조건을 가진 함수로, 두 입력 값 사이의 차이에 대한 변화율이 제한되어 있는 함수이다. 이런 가정은 시스템 동역학이 지역적으로 안정되어 있다는 가정으로도 볼 수 있다.
시스템을 안정화 시키는 목표 : 비선형 시스템을 0으로 안정화 하는 컨트롤 목적이 있다하자. 이는 단순히 positive definite function V를 0으로 만드는 피드백 제어를 찾으면 된다. (여기서 V는 energy function)

입력이 k(x)일 때 위의 조건이 성립하면, 이때 V(x,k(x))는 아래와 같고 감마는 양수이다. 리아프노프 이론의 변화율 조건을 생각하자.

그러면 시스템은 V(x*) = 0에서 안정화 된다. 즉, x* = 0으로 수렴하게 된다. 감마의 경우 0보다 큰 모든 양의 실수에 속한다. 감마(0)의 경우 0 이 되고, 이는 감마가 단조함수라는 뜻이된다. r1 < r2 일 때 감마(r1) < 감마(r2)라는 뜻.
즉, 안정성을 찾는 건 단순하게 V 함수의 변화율이 음수인 경우를 찾으면 된다.
실제로 시스템이 안정화 되려면 피드백 제어 입력을 명시적으로 설정할 필요는 없고, 단순히 제어기가 V함수의 변화율 조건만 만족하면 됐다. 정확하게는 V가 positive definite이고 아래 조건을 만족한다면 CLF가 된다.
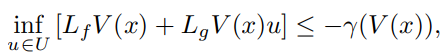
이게 중요한 이유는 모든 x에 대해서 모든 set의 안정화 시키는 컨트롤러를 고려할 수 있게 해주기 때문이다.
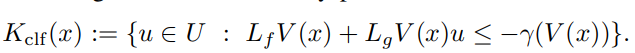
위 Kclf 집합은 제어 입력 u로 정의 된다. 이 집합은 affine contrain이 걸려있다. 따라서 최적화 기반 제어기를 설계할 수 있게 해주는데, 이는 V가 CLF인 조건을 설명하기도 한다. 예를 들어

일 때, 안정화 시키는 제어기가 있다는 건 쉽게 알 수 있다. 어쨌든 중요한 건 V 함수가 CLF인지 아닌지에 따라 안정화 가능한 제어기가 있냐 없냐가 갈린다는 사실이다.

최종적으로 정리1번이 나오게 된다.
Control Barrier Funtions
안정성은 시스템이 특정 포인트로 가게 만드는 거라면, 안전성은 safe set을 나가지 않게 하는 것이다. 여기서는 연속 미분 함수 h의 superlevel set으로 C 집합을 정의한다. 이에 따라 아래 형태를 safe set이라 정의한다.

제어 입력 u = k(x) 를 피드백 제어기라 하고 아래 다이나믹 시스템이 로컬 Lipshitz라고 하자.
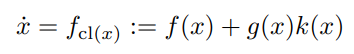
(로컬 Lipshitz란, 특정 지역에서 기울기의 크기가 일정하게 제한되어 있다는 것을 의미한다.)
안정성이란, 로컬 Lipshitz 가정 때문에 어떤 초기 조건이라도 해당 시스템이 특정 시간 간격 동안 안전하게 진행될 수 있으면 나타낸다. 논문에서는 초기 조건에 대한 최대 존재 구간이 있다고 설명하며, 구간 내에서 x(t)는 위 식의 고유 해이며 fcl이 forward complete한 경우에는 tau_max가 무한으로 간다고 했다. (사실 이 부분이 뭔소리지는 모르겠음. forward complete?, 아마도 인터벌 구간이 무한대로 된다 라는 뜻 같음)
이런 경우에 시스템을 safe하다고 정의할 수 있게 된다.

최종적으로 정의 1번이 나오게 된다.
CBFs에 대해 알아보자.
CLF를 참고해서 safety를 고려해보자. 논문에서는 너무 리아프노프를 참고해서 일반화하지 말라고 한다.
기본적으로 CLF V가 존재하여 V(x) = 0이고 superlevel set은 C를 가지면 이 컨트롤러는 ss C를 불변하게 만들어서 C가 안전하게 되긴 할 거다. 다만, 너무 제한적이라서 c아래의 값들 , 즉 sublevel set의 c 들도 전부 불변하게 만들게 된다. 따라서 논문에서는 positive definite function을 필요하지 않으면서 set 불변성을 가져가려 한다. h가 CBFs로 작용하려면 C를 불변하게 만들지만 h의 sublevel set은 불변하게 만들지 않아야 한다는 뜻이다.
시작하기 앞서, extended class Kinf 함수에 대해 정의하고 간다. 이때 함수는 모든 실수에서 증가하는 단조함수의 형태를 띈다. 물론 0에서 0이라는 조건도 있다.
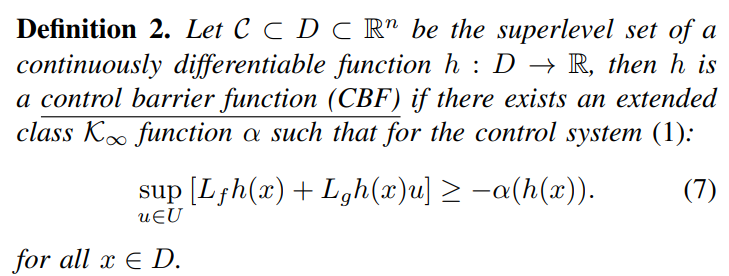
이제 정의 2에 대해 이야기 해보자. 위에서 얘기했던 것들을 조합하면 정의 2가 나온다.
기본적으로 시스템 공간 D가 n차원의 부분집합이며, 특정 조건을 만족하는 안전영역 C가 D의 부분집합이 된다. 이때 h는 D에서 정의 된 실수 공간으로서의 연속 가능한 미분 함수인데, h가 안전 영역 C의 superlevel set인 경우 h를 CBF라고 한다. 단, CBF라고 하기 위해서는 extended class kinf 함수 알파가 위에서 이야기했던 x=f+gu 형태의 제어 시스템에서 존재해야 한다. (f와 g는 로컬 Lipschitz 함수라는 걸 기억하자).
이런 경우 h값을 이용해서 제어 입력을 선택할 때 시스템이 안전한 상태로 유지되는 부등식 조건을 만족하게 된다. (sup의 경우 해당 식에서 최대값을 확인하는 것이다. 즉, h값을 이용한 알파 함수보다 무조건 클 경우 안전하다고 한다는 뜻)
CBFs를 통해 Safety를 보장 할 수 있다.
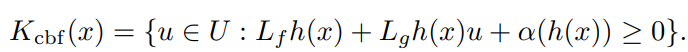
Kcbf(x)는 상태 x에서 시스템을 안전하게 유지하는 데 사용 가능한 모든 제어 입력의 집합이다. 이는 위의 조건을 만족하는 모든 u로 정의 된다.

따라서 정리2번은 C가 연속 미분 가능 함수 h의 superlevel set으로 정의 된 안전한 영역인 경우, h가 D에서 CBF이며 경계C에서 h의 편미분이 0이 아닌 경우 Kcbf(x)에 포함되는 Lipschitz 연속 컨트롤러 u(x)는 시스템을 안정하게 만든다. 추가로 C는 시스템 공간 D내에서 점진적 안정적이다. Remark 5에 의하면 gradient h가 경계선에서 사라지지 않는 게 0이 h의 regular value인 경우와 동등하다고 한다. 이 조건은 안전성 정리에서 특별 조건은 만족시키는 데 필요 조건이다.
Remark 6에서는 안전한 set C가 단순 불변이 아니라 점진적 안정적이라는 것도 강조한다. 즉, 안전한 set C를 벗어나지 않으면서도 C로 수렴이 보장된다는 뜻이다. 실제 이를 구현하게 되면 시스템이 모델링 오류나 노이즈로 안전한 집합을 벗어나는 경우가 생길 수 있는데, CBF 정리의 결과로 Kcbf 컨트롤러는 시스템을 다시 안전한 집합 C로 유도할 것이기 때문에 안전하고 안정한 시스템 구현을 보장하게 된다는 것이다.
Necessity for Safety
CBFs가 C set에 대한 합리적인 가정이 있을 경우 safety에 대한 강력한 필요충분 조건을 제공한다는 것을 확인할 수 있다.

정리3을 보자.
C를 연속 미분 가능 함수 h의 superlevel set이라고 하고, 이때 h는 경계 x에 대한 편미분이 0이 아닌 경우이다. 만약 제어 입력 u = k(x)가 C 영역을 안전하게 만든다면, C는 forward invariant하다. 그러면 h는 C에 대한 CBF가 된다.
CBFs가 안전성에 대한 필요 충분조건을 제공해줬다면, 과연 우리는 어떻게 컨트롤러를 합성할 수 있을까? 가장 최소한으로 기존 컨트롤러를 수정하는 것을 목표로 할 경우 당연하게도 최적화 기반의 컨트롤러를 고민하게 된다.
Safety-Critical Control
피드백 컨트롤러 u = k(x)가 있다고 하자. 이때 k(x)가 Kcbf에는 포함되지 않는다고 할 때 safety를 보장하도록 제어기를 변경해보자.
Kcbf에 대한 안전성 조건은 u에 대한 affine이라는 걸 알 수 있다. 따라서 u에 대한 최소한의 변화를 찾는 QP 기반 제어기를 고려할 수 있다.

CBF-QP에서는 inequality 제약 조건이 1개 밖에 없기 때문에 input 제약 조건이 없을 경우 CBF-QP는 closed-form 해를 가지게 된다(KKT조건에 따라 최소 놈 컨트롤러 형태)
Unifying with Lyapunov
안전성과 안정성을 통합하는 방법으로 QP기반의 safety-critical 컨트롤러를 제안한다. 처음 최적화 기반의 컨트롤러는 CLF의 맥락에서 다중 목적 비선형 제어를 위해 도입됐었다. 안정성과 토크 제약조건을 합치는 것과 같은 작업을 했는데, 아래와 같은 QP 형태를 제안했다.

H함수는 positive definite matrix 이며, 델타는 QP의 solvability를 고려하여 보장해주는 relaxtation variable이며 p>0의 패널티를 받는다. (무슨 뜻인지 잘 모르겠다, 논문에서는 stability에 대한 조건을 완화해서 safety를 보장하기 위한 작업이라 한다.)
CBFs FOR SYSTEM WITH ACTUATION CONSTRAINTS
비선형 affine 제어 시스템을 생각해보자. performance function ρ를 통해 정의 된 허용가능한 집합(alloable set) 상태 A가 있다고 하자. 아래와 같이 표현한다. (performance function이란 단순히 어떤 시스템의 성능 혹은 좋은 정도를 측정하는 함수라 생각하면 된다.)

이때 CBFs를 통해 하고 싶은 작업은 CBF h의 superlevel set인 C를 실수에 속하는 h 함수를 만들어서 상태 A 집합에 속하게 하는 것이다. (논문 표현이 좀 이상한데, D 2개아 아니라 C랑 D 여야 할 것 같은데..흠)

당연하게도 위에서 이야기한 정의2를 만족한다면 A에서의 ρ(x)와 h(x)가 같아질 수도 있다.
하지만 논문에서는 A가 불변이지 못하는 경우를 이야기 한다. 대신 허용 가능한 집합 중에 safe 부분 집합을 찾아야 한다. 이때 A가 불변하지 못하는 이유는 제어 입력 자체를 제한하는 제어 집합 U 때문이거나, 상대적 자유도가 높은 동역학 시스템이기 때문이다.
로컬 Lipschitz 비선형 제어기 알파가 있다고 하자. 알파가 초기 조건에 대해 허용 가능한 제어 영역에서도 움직일 거라는 건 알 수 있지만 safety를 보장한다는 건 알 수 없다. 아래와 같이 미분 방정식을 만족하는 시스템이 있다 하자.

성능 함수와 베타를 이용해서 Barrier function을 계산할 수 있다.

h 함수는 일반적인 제어 입력 알파 경로에 대한 성능 함수의 값을 상한, 하한으로 제한 하는 형태로 만들어진다. 따라서 입력값 자체가 일정한 한도를 가진 형태로 들어가게 되어 안전을 보장하게 된다. 정리하면 아래 정리 4가 된다.

이때 h 함수 자체를 closed form 형태로 계산하는 것도 가능할 수도 있다. (참고 : https://ieeexplore.ieee.org/document/8511342)
closed form이 아닌 근사할 수도 있다. 일정 horizon동안 시스템 경로를 시뮬레이션하고 상한, 하한을 수치적으로 계산하면 된다. 다만 CBF-QP를 하게 되면 h의 gradient를 구해야 하는데, 이는 gradient 또한 근사해야하는 작업이 필요하게 된다. 이는 차원의 저주에 빠질 가능성이 있다는 뜻.
또 다른 방법은 h를 파라미터화 하고 보수적인 h를 찾는 방법이다.
고정 된 차원의 다항식과 sums-of-squares 방식을 이용하여 h를 파라미터화 할 수 있다.
너무 길어져서 Exponential control barrier function은 추후에 Exponential control barrier functions for enforcing high relative-degree safety-critical constraints를 리뷰하는 걸로 하자.
'미니멀공대생 > Control' 카테고리의 다른 글
| [논문리뷰] Prehensile Pushing : In-hand Manipulation with Push-Primitives (1) | 2024.03.14 |
|---|---|
| Integral Adaptive Law와 Persistent Excitation에 관하여 (2) | 2024.03.08 |
| [논문리뷰] Deformable object manipulation :: Modeling 파트 (3) | 2023.10.15 |
| ROS2 :: Moveit2 - Hybrid Planning에 관하여 (2) | 2023.06.13 |
| ROS2 :: Moveit2 Python API에 대해 알아보기 (Rolling) (0) | 2023.05.22 |
