티스토리 뷰
[논문리뷰] Prehensile Pushing : In-hand Manipulation with Push-Primitives
미니멀공대생 2024. 3. 14. 18:07Prehensile pushing: In-hand Manipulation with Push-Primitives
저자 : Nikhil Chavan-Dafle and Alberto Rodriguez
논문 : https://dspace.mit.edu/handle/1721.1/98114
작성 : 이해구
물체를 잡고 있는 그리퍼가 있고, 물체와 닿아 있는 환경이 있다.
즉 최소 물체에는 접촉점이 3개가 있게 된다. 우리가 물체를 움직이게 싶다면 접촉점 3개에 힘을 가하면 된다(힘을 발생 시킨다).접촉점에 힘을 가하려면 우선 접촉 모델이 있어야 한다. 접촉 모델은 접촉에 의해 생긴 기하학적인 조건과 마찰 조건의 특징을 나타내고 이들이 물체를 집었을 때의 안정성과 물체의 움직임에 주는 영향을 나타낸다.
prehensile manipulation라는 내용으로 접촉점에서의 미끄러짐을 용인하고 in-hand manipulation을 연구한 논문들이 있다.
특정 논문에서는 집은 물체의 방향을 주변 환경과의 접촉을 통해 변경하는 연구 내용을 보인다. 이 논문에서는 물체에 항상 붙어(stick) 있는 외부 접촉점으로 부터 "이상적인" 외부 wrench를 이용한다. 이와 비슷하지만 다르게 다른 논문에서는 실제 외부 푸셔(PUSHER)가 외력 wrench를 만드는 형태로 연구를 진행한다. 이를 위해 지역 접촉힘과 외부 접촉점에서의 상대적 가속도를 계산한다.
특정 논문에서는 툴 힘에 반대로 고정 된 부분의 안정성을 연구 하고 놓치지 않기 위해 고정부(그리퍼)의 집는 힘을 예측하였다. 이 연구 목적은 단순히 힘의 평형을 유지하여 미끌어짐을 방지하는 것이기 때문에 quasi-static 분석이 충분했지만, 다른 논문에서는 pusher의 모션과 힘의 불평형에 의한 특정 접촉점에서 의도적인 미끌어짐에 대한 분석을 하기 위해 quasi-dynamic을 가정하였다.
prehensile pushing은 non-prehensile와도 크게 관련이 있다. 일반적으로 Non-prehesile이 평면에서 물체를 미는 작업일 경우 물체와 바닥면에서의 면접촉에 생기는 압력 분포의 불확실성은 pusher에 의해 제어 가능하고 예측 가능한 모션으로 제한 된다.
논문들에서는 여러 조건들을 가정한다. 가정 조건들을 살펴보면
- 물체의 모양과 무게를 알고 있다.
- 물체와 그리퍼 간의 접촉 정보를 알고 있다. (위치, 기하학정보, 마찰)
- 그리퍼의 기구학 정보를 알고 있다. 또한 이는 액추에이터부터 접촉 속도의 자코비안 형태로 알고 있다.
- 그리퍼 힘의 크기를 알고 있다.
- 외부 푸셔의 모션, 마찰 기하학정보 위치를 알고 있다.

위 사진과 같은 3차원의 경우에는 각 접촉이 접촉 모델에 기반하여 추가적은 마찰힘과 모먼트를 만들어 낸다. 이때 제어적인 측면에서 원하는 것은 푸셔에서의 가장 작은 수직힘을 찾아 집고 있는 물체를 움직이게 하는 것이다. 그 순간의 물체 움직임 방향을 아는 것이다.
아래와 같은 조건들을 고려하여 문제를 접근하였다.
- f_i, f_ext : 그리퍼와 물체와 외부 푸셔와의 접촉 포인트에서의 힘
- a_i, a_ext : 각 접촉에서의 상대적 가속도
- a_obj : 물체의 가속도
그리고 제약 조건들은 아래와 같다.
- 뉴턴 역학 : 물체의 가속은 내부 집는 힘, 외부 푸셔와 중력 힘이 만든 전체 wrench에 의해 만들어진다.
- 강체 제약 : 접촉에서의 가속은 물체에 따라서 있어야 한다.
- 단방향 접촉 제약 : 접촉은 오직 밀 수만 있으며, 접촉이 유지 되는 경우에만 가능하다.
- 마찰 힘 제약 : 각 접촉에서 normal force와 tangential frictional force 그리고 tangential 가속도는 쿨롱 마찰법칙과 최대 에너지 소산을 만족해야 한다.
- 복잡한 접촉에 의한 제약 : 복잡한 형상의 기하도 마찰 포인트가 있는 강체의 집합으로 모델링한다. 각 구성 점의 객체와의 개별 상호작용은 patch의 강체성으로 봐야한다.
- 푸셔의 모션에 대한 제약 : 집는 작업이 무너지면 (완벽히 집은 상태가 아니라는 뜻), 물체는 푸셔의 모션을 따라야 한다, 즉 접촉에 대한 상대적 normal 가속은 푸셔의 모션을 따라야 한다.
Contact modeling
이제 Contact modeling을 진행해보자.
상호작용에서의 마찰 모델을 정확히 만들기란 어렵다. 하지만 접촉 모델은 간단하며 계산이 쉬우며 직관적이다. 접촉 모델은 접촉이 힘과 토크를 전달할 수 있는 방향을 정의한다고 보면 된다.
간단한 모델은 3가지가 있다.
- 마찰이 없는 포인트 접촉 : 힘을 접촉면에 normal방향으로만 보낸다.
- 마찰이 있는 hard 포인트 접촉 : normal 방향과 2개의 tangential 방향으로 힘을 보낸다. 하지만 토크는 없다.
- 마찰이 있는 soft 포인트 접촉 : 3가지 방향은 위와 같지만, contact normal로 torque를 보낸다.
논문에서는 접촉 힘을 3개의 단위 벡터와 그의 크기로 표현한다.

쿨롱의 마찰 법칙은 전체 접촉 힘이 아래의 집합에 있는 경우 만족하게 된다. 마찰 원뿔 안에 있는 경우를 말한다. (FC for Friction Cone)

이때 마지막 inequality condition이 equality condition이 되는 경우는 접촉에서 상대적인 모션이 있는 경우이다. 즉 접촉면에서 미끌어진다는 뜻이다.
Friction cone은 계산이 어렵기 때문에 이를 선형 근사 한다. 원뿔을 여러면을 가진 다각형으로 만들게 된다. 접촉면에서의 tangent plane을 표현하는 t, o벡터를 d 단위 벡터로 표현한다.

따라서 friction force를 양의 선형 조합식으로 표현할 수 있게 된다.

최종적으로 전체 접촉 힘은 로컬 좌표계에서 하나의 행렬로 표현될 수 있다.

D 행렬에 선형 근사 된 마찰 원뿔의 단위벡터를 모으고, 크기를 하나의 행렬에 모아서 선형 근사한 마찰 원뿔식을 표현하면 아래와 같다.
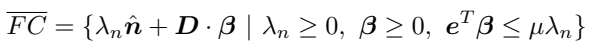
쿨롱의 법칙은 접촉에서 상대적 모션이 있고, 꼭 그럴 때만 마찰 힘은 마찰 원뿔 위에 있어야 한다고 정의한다. 이를 위해 논문에서는 여유 변수를 하나 설정하여 직관적으로 접촉에서의 상대적 수직 방향 가속 크기를 표현할 수 있도록 한다.

이는 접촉에서 상대적 모션이 있을 경우 (zeta > 0), 마찰 힘이 마찰 원뿔의 모서리에 있을 수 있다는 걸 보장한다. (mu * 알파 - e*beta = 0)
Maximun Dissipation Principle(최대 소산의 법칙..?)의 선형 근사
최대 소산의 법칙은 각 접촉에 대한 마찰 힘과 모션에 관련이 있다. 마찰은 꼭 에너지 소산을 최대화하는 방향으로 전달된다는 뜻이다. 직관적으로는 모션의 반대 방향으로 마찰이 작용한다는 뜻. 논문에서는 선형 상보 조건으로 표현한다.

이때, 제타는 접촉에서의 상대적 수직방향 가속의 크기를 근사하고, a벡터의 경우 원뿔 근사 방향 벡터의 상대적 가속을 근사한다(?). 위에서 언급한 조건들이 마찰 힘이 반대 수직 방향 가속을 최대로 만들고, 접촉이 미끌어지면 원뿔 근사의 방향 벡터 중 하나가 가속 방향이 되게 된다.
Contact with non-trival Geometry
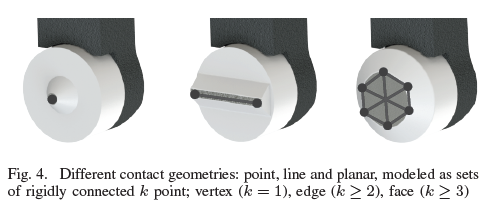
논문에서는 Contact시 단순히 single point contact을 가정하는 것이 실제 환경에서 동일한 물리 현상을 제현할 수 없다고 한다. 선과 평면 접촉의 경우 점 접촉보다 기구학적으로 모션을 제약한다. 또한 normal 힘이 비정형적으로 분산되기 때문에 마찰 힘은 접촉이 있는 강체들의 모션에 더욱 영향을 받게 된다. limit surface와 같은 방법으로 접촉 모델을 고도화 할 수 있지만 계산량이 너무 많다.
논문에서는 점과 라인, 평면을 몇개의 접촉 집합으로 나눠서 근사한다. 또한 각 접촉들은 강체로 이어져 있다 가정하기에 상대적인 가속도와 normal 힘이 다른 접촉 부분에서 다르지 않을까라는 고민을 할 필요 없다. 일반적으로 m차원의 접촉에는 k의 포인트로 구성된다.
논문에서는 아래 내용들을 정하여 진행한다. (Impose)
- k 마찰 원뿔과 k 최대 소산은 각 구성 접촉마다 하나씩 각각의 힘과 가속도를 관련 짓는다.
- 3k−m−4 는 k 구성 점들의 가속도와 관련 된 독립적인 제약조건들로 이들이 서로 견고하게 부착되어 움직이도록 강제한다. (?) 예를 들어 라인 접촉의 경우 가속도와 구성 포인트가 a1, a2, p1, p2로 표현된다. 이때 어떤 구성 포인트 pj의 가속도 aj는 어쨌든 아래 식을 만족해야 한다.

이때 라인은 차원 m=1이기 때문에 3(k-2)=3k-6 제약 조건을 만든다. (? 논문이 조금 이상한 듯, 위에는 3k-3이 맞는데..)
(Contact with nontrivial Geometry는 조금 더 공부해보는 걸로, 잘 이해가 안된다)
Grasp Modeling
접촉시에 first order 안정성에 행렬 분석의 사용을 정리한다. 외부 푸셔 효과 고려를 자세히 다룬다. p1~pn은 내부 접촉, pext1~pextm을 외부 점 접촉을 나타낸다.
Grasp matrix(gm으로 축약) G는 물체 참조 프레임에서 접촉에 의해 물체로 전달 가능한 모든 wrench의 범위를 정의한다. 접촉 pi에 대해서 gm Gi = [ni, ti, oi]는 선형적으로 힘의 집합을 늘리고, 접촉 i는 이를 물체로 전달이 가능하다. 이때 접촉 pi로 인해 물체로 전달되는 힘은 아래 식으로 나타낼 수 있다.
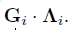
모든 접촉에 대한 Gi를 연결시켜 하나의 G 행렬을 만들게 된다. 람다 또한 같은 작업을해서 람다 행렬을 만든다. 이런 작업들은 마찰 원뿔의 polyhedral 근사에도 적용될 수 있다. G_ 행렬은 이제 contact i가 물체로 전달할 수 있는 힘의 집합의 범위가 되고, 람다_ 는 그에 대응하는 크기 열벡터가 된다.

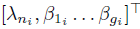
최종적으로 물체에 적용되는 전체 wrench는 G_와 람다_의 곱으로 이뤄진다.
이를 통해 집는 동작이 안정 된 조건을 표현할 수 있다. (물체에 힘의 평형이 이뤄진 상태)
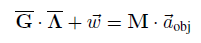
Hand Jacobian
Hand Jacobian 행렬은 조인트 액추에이터의 모션을 접촉 점의 지역 모션으로 매핑한다. 논문에서는 액추에이터마다 Ji가 한개의 열을 가지게 되고, 액추에이터가 만드는 로컬 frame에서 점 접촉 pi에서의 지역 속도를 표현한다. 설명이 좀 어색한데, 쉽게 말해 액추에이터가 움직일 때 접촉에서의 속도를 나타내도록 자코비안을 만들겠다는 거다. 논문에서는 외부 푸셔에 대한 효과를 포함시켜 자코비안을 구성한다.

가상의 액추에이터를 모델링하고, 첫번째 외부 접촉의 자코비안을 단위행렬로 나타낸다.
그 외 다른 점 접촉들은 첫번째 접촉으로 부터 자신들의 로컬 프레임까지의 기구학 관계에 의해 결정된다.
이는 처음에는 무슨 소리인지 몰랐는데, 아마 선이나 면접촉인 경우를 말하는 것 같다.
Contact acceleration
접촉에서의 가속도는 물체와 푸셔 손의 가속도와 연관이 있다. 2개의 관점에서 접촉 점의 모션을 바라볼 수 있는데,
- 물체의 관점에서 : gm은 물체의 가속도를 모든 접촉점의 가속도의 관계를 표현한다. G.T*a_obj으로 계산된다.
- 손의 관점에서 : hand jacobian이 엑추에이터의 가속과 모든 접촉에서의 가속의 관계를 표현한다. J*theta''
이때 theta''은 그리퍼 액추에이터의 모션도 포함하고 있고 논문에서는 따로 필요하지 않기에 0으로 설정한다.
또한 가상의 액추에이터 푸셔는 자코비안이 단위 행렬이 된다.
최종적으로 이 식들의 관계를 전부 정리하면 :

즉, grasp에서 발생하는 물체의 가속도와 hand가 움직여 발생하는 가속도 간의 차이가 접촉점에서의 가속도가 된다.
Prehensile pushing
논문에서는 미는 동작이 정적 grasp 상태에서 시작하고, 미는 속도가 매우 빨라 마찰 힘이 이너시아를 이기는, 즉 quasi-dynamic 이라 가정한다. 이런 가정은 제약조건을 접촉 힘과 접촉 가속도로 표현할 수 있게 한다.
Constraints
뉴턴 역학
미는 힘에 반응하여, 모든 접촉은 마찰 힘을 발생하게 된다. 뉴턴의 법칙에 따라 물체의 가속도는 손가락 힘과 푸셔 힘 그리고 중력에 의해 생기는 물체의 wrench에 따라야 한다. 힘의 불평형식은 아래와 같이 표현된다.

Rigid body constraints and Motion of the pusher
물체는 강체기 때문에 모든 접촉은 동시에 움직여야 한다. 아래 식은 모든 로컬 접촉 가속도 a를 물체와 푸셔의 가속도로 표현한다.

Frictional force
앞선 내용을 참고하면 된다.
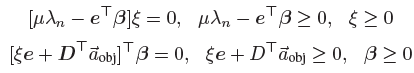
Optimization problem
앞서 언급한 제약조건들이 접촉 힘, 접촉 가속도, 물체의 가속도에 대한 solution space 를 정의하게 된다. 논문에서 접근하는 문제들은 추가적인 선형 제약을 가 linear complementarity problem의 형태를 가지고 있다. (mixed LCP로 몇몇 변수들은 상보적 제약조건과 연관이 있지만, 몇몇은 그렇지 않다). 논문에서는 이를 qp로 변형하여 해결한다. 모든 상보제한 조건들을 2차 cost 함수로 변경하고 선형 eqaulity, inequality 제약조건을 만들어 convex solution space를 만들었다 한다. 모든 상보항이 양수여야 하며, 이들 제한 조건이 0으로 갈 때 가장 최소가 된다.
최적해를 찾게 되면 이는 물체를 움직이기 위해 필요한 푸셔의 힘과 손의 모션을 알려준다.
MCube Lab이 In-hand manipulation쪽으로 연구를 오랫동안 많이해왔다. 여기 논문들만 잘 읽어도 능력치가 많이 향상될 것 같은 느낌. 이제 논문 구현을 해보자.
'미니멀공대생 > Control' 카테고리의 다른 글
| [MCube-MIT] Manipulation 연구 정리 (0) | 2024.04.15 |
|---|---|
| [논문리뷰] In-Hand Manipulation via Motion Cones (1) | 2024.03.22 |
| Integral Adaptive Law와 Persistent Excitation에 관하여 (2) | 2024.03.08 |
| [논문리뷰] Control Barrier Functions : Theory and Applications (1) | 2024.01.03 |
| [논문리뷰] Deformable object manipulation :: Modeling 파트 (3) | 2023.10.15 |
