티스토리 뷰
Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(2) :: 접촉 시뮬레이션
미니멀공대생 2024. 9. 20. 17:12LCP를 이용해서 Contact model을 구성하는 내용을 다뤘었다. 오늘은 실제 LCP 문제를 푸는 법에 대해 이야기 해보려 한다. 기본적인 LCP는 아래와 같이 정의 된다.

이런 형태로 접촉 문제를 구성하여 LCP를 풀면 접촉 힘을 계산할 수 있게 된다. 우선 간단한 점이 바닥과 접촉하는 경우의 Contact model을 구성해보자. (원이 아니라 점이다. Point mass라 생각하자.)

무게는 0.2, 마찰 계수는 1이라 하자.
점이기 때문에 Mass matrix, (혹은 Inertia matrix)는 무게를 대각행렬로 가지는 형태가 된다.
점이기에 바닥과 접촉하는 순간 발생하는 접촉의 수는 1개로 고정된다.
우선 모든 걸 contact frame (접촉 프레임)으로 바꿔줘야 한다. 어떤 좌표 혹은 공간들의 변환/매핑은 자코비안으로 한다고 생각하면 된다. (조인트 공간에서 카타시안 공간으로 매핑하는 게 우리가 흔히 알고 있는 자코비안이듯이)
접촉 자코비안은 아래와 같이 표현한다.
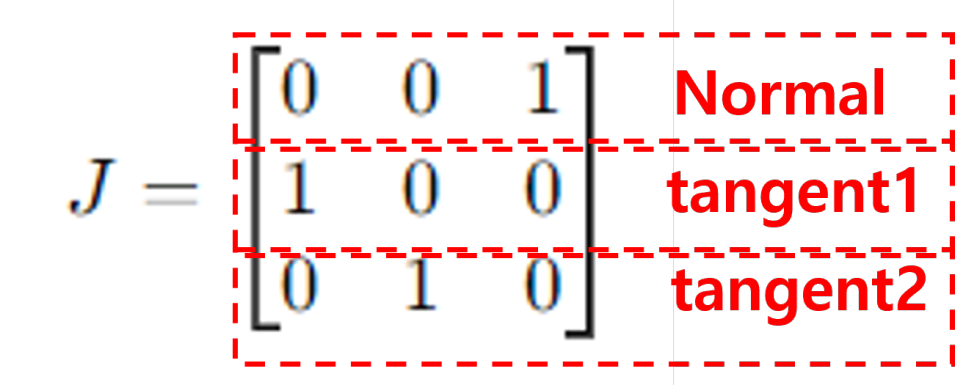
접촉 자코비안
매우 간단하다. 각 행별로 수직 방향, tanget 방향, tanget 방향을 뜻한다. 순서를 꼭 기억하자. normal 방향이 먼저오기 때문에 자코비안과 곱해지는 무엇이든 가장 먼저 수직 방향의 성분들이 나오게 된다. 자코비안 * 물체의 속도를 하게 되면 수직방향 속도, x방향, y방향의 속도가 나온다고 생각하면 편하다.
접촉 자코비안을 구성하였다면 우리가 원하는 문제는 LCP 형태로 구성해야 한다. LCP를 풀었을 때 우리가 원하는 결과는 접촉 모델이 고려 된 이후의 물체의 속도이다. 즉, 물체의 Dynamics 안에 Contact force가 계산되어 이를 적용한 물체의 동작이 최종 결과이다.
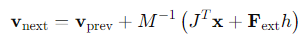
LCP Solver의 최종 결과
1편에서 봤던 내용을 기억해보자. 우리는 총 3 방향에 대한 LCP를 만든어 1개의 LCP로 묶어서 풀어야 한다.

첫번째 LCP로 충돌 관계에서 두 물체 간의 상대 속도에 관한 LCP이다.

두번째 LCP는 tangen 방향이 maximum dissipation이 되는 방향으로 선형 근사를 하도록 한다. (이 부분이 잘 이해가 안가지만..패스)
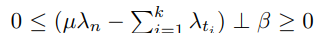
마지막은 마찰힘이 Coulomb friction cone으로 제한되도록 한다. 이때 베타가 >0 이냐 =0 이냐에 따라서 마찰 상태가 sliding이냐, stick이냐가 바뀔 수 있다.
이 3개의 LCP를 1개의 행렬로 묶어서 하나의 LCP 형태로 표현해보자. 시작은 이진화 된 뉴턴 오일러 방정식으로부터 한다. 접촉에 대한 속도-임펄스 식을 표현하면 아래와 같다.

람다는 임펄스를 표현하고, b는 초기 속도이다. 따라서 v는 임펄스가 작용했을 때의 속도를 뜻한다.
각 방향의 초기 속도를 나타내는 b 벡터는 아래와 같이 표현된다.

임펄스와 속도를 매핑해주는 A 행렬은 아래와 같이 표현된다.

이때 각 B요소들은 contact frame에서의 Mass matrix의 역행렬이다. 한가지 참고할 점은 A행렬이 non-symmetric이라는 점이다. 이로 인해 Proejcted Gauss-seidel 방식을 사용할 수 없게 된다. 그 대신 Lemke 방식이나 Newton기반 방식을 사용해야 한다. (maximum dissipation을 무시하고 PGS 방식으로 접근할 수도 있다.)
이를 최종적으로 정리하면 아래와 같이 표현된다.

우리가 원하는 접촉 현상을 LCP 형태로 만들었다. 이제 이 LCP를 Lemke 방식으로 풀어주면 된다. 우리는 위 식에서 A와 b를 알고 있고, x를 찾으려 한다. 이를 시작부분에서 언급한 LCP 문제로 대입하여 확인하면 M = A, q = b가 있고 z를 구하면 된다. Lemke 방식은 따로 알아보지않고, 구현되어 있는 코드를 사용하여 시뮬레이션 하면 된다.
제어 입력은 [-1; 0; 0]과 [-3; 0; 0] 으로 주고 중력이 작용한다고 하자.
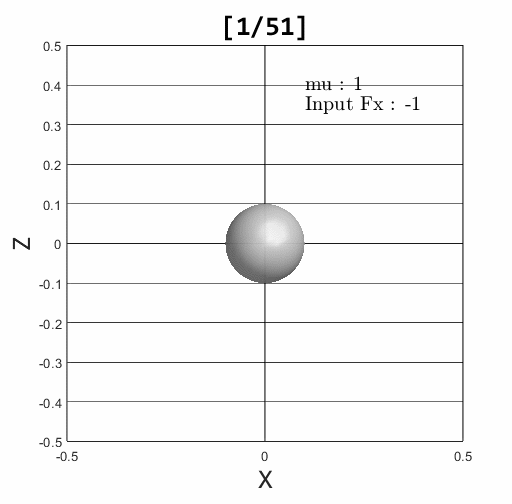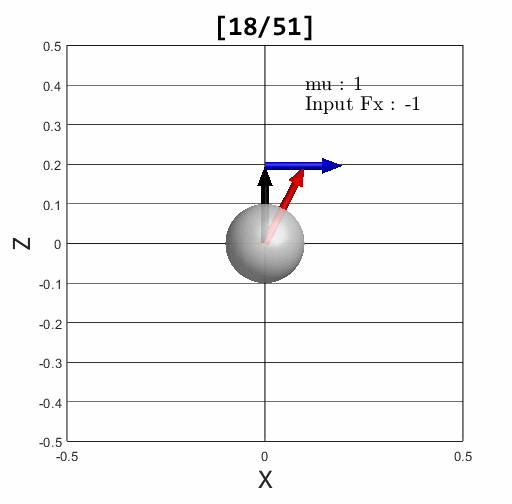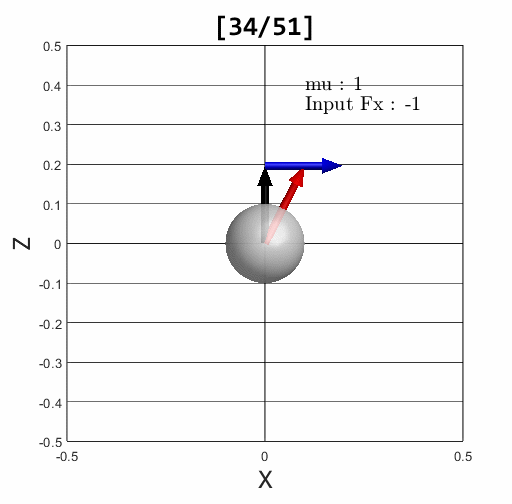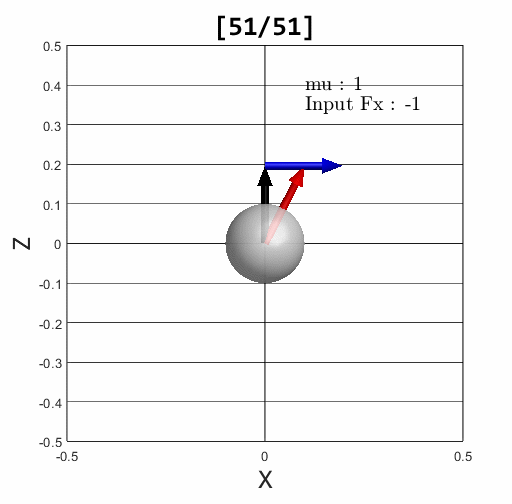
마찰력이 마찰 원뿔 안에 있는 경우 Stick condition

마찰력이 마찰 원뿔 밖에 혹은 경계에 있는 경우 Slip condition
입력 된 힘에 따라 계산 된 접촉 힘이 마찰 원뿔 안에 있는 경우와 그렇지 않은 경우를 확인할 수 있다. 검은색은 법선 방향 힘, 파란색은 마찰 원뿔, 빨간색은 계산 된 접촉 힘을 표현한다.
LCP를 이용한 contact model의 중요점은 stick과 slip 조건을 확인할 필요가 없다는 점이다. 접촉 힘이 문제없이 계산 됐다면 그에 맞는 마찰력도 게산되어 stick 상태인 경우에는 입력 힘을 상쇄하여 속도가 0이고, slip 상태인 경우에는 접촉 힘보다 작은 마찰력이 되어 밀리는 상황의 속도를 계산하게 된다. 즉 접촉 힘를 가지고 마찰 원뿔을 넘었는지 안넘었는지 매번 확인하지 않아도 된다는 뜻.
단순 LCP를 사용한 접촉 모델은 기초일 뿐이긴 하다. 그나마 최신 접촉 모델에 대한 내용은 MuJoCo에 적용 된 접촉 모델을 설명하는 Convex and analytically-invertible dynamics with contacts and constraints: Theory and implementation in MuJoCo을 읽어보면 좋다.
참고자료
An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Coulomb Friction
A convex smooth and invertible contact model for trajectory optimization
https://github.com/erwincoumans/contact_models
'미니멀공대생 > Control' 카테고리의 다른 글
| Trajectory optimization 사용 후기 혹은 Tips & Tricks (2) | 2025.01.20 |
|---|---|
| MuJoCo :: SDF와 자세한 Collision mesh 만들기 (2) | 2024.10.20 |
| contact model, contact force 기초 논문 (0) | 2024.09.19 |
| Linear Complementarity Problem을 이용한 접촉 모델(Contact Model)(1) (2) | 2024.09.12 |
| Homotopy path planning(호모토피 경로 계획) (0) | 2024.09.07 |
