티스토리 뷰
참고한 모든 Paper는 아래 링크에 있습니다. 도움이 되셨다면 Star를 눌러주세요 ㅎ
GitHub - benthebear93/awesome-mobile-manipulator: Reading List and related repos for mobile manipulator
Reading List and related repos for mobile manipulator - GitHub - benthebear93/awesome-mobile-manipulator: Reading List and related repos for mobile manipulator
github.com
해당 글은 아래 논문을 정리한 내용입니다.
참고 논문 : Kinematic Control of Redundant Mobile Manipulators by Mashali, Mustafa
모바일 매니퓰레이터는 두개의 독립적인 경로(Trajectory)가 있다. 로봇 팔 끝단(EE)의 경로와 모바일 플랫폼의 경로인데, 복잡한 테스크를 진행할 경우 두개의 경로는 동시에 작동되어야 한다. 다만, 로봇 하드웨어에는 항상 제약(제한)이 있고 특정 상황에서는 두개의 경로를 동시에 따라갈 수 없을 수 있다. 이를 해결하기 위해서는 우선이 되는 경로를 먼저 정하고, 다른 경로는 어느정도 에러를 용인하도록 해야한다.
이번 글에서는 이를 위해 목적(Task)의 우선순위(Priority)를 변수를 통해 정하는 방식에 대해 설명하겠다.
먼저 제일 높은 우선순위를 가지는 경로의 경우 fully defined 된 형태이다. 하지만 다른 경로의 경우 하드웨어 제약에 맞게 defined 된 상태가 된다. 이때 3개의 변수가 사용되는데 이들은 모바일 플랫폼의 경로를 EE 경로에 대해서 혹은 그 반대에 대해서 정의하는 데 사용 된다.
(추가로 이 변수들은 로봇 팔의 조인트 각도와 모바일 플랫폼의 모션과 연관이 있다.)
참고 논문 : Task priority based dual-trajectory control for redundant mobile manipulators
이 논문에서는 싱귤러에 강건하고 Task 우선순위에 맞는 gradient projection 방식 inverse를 사용한다, 이를 사용해서 manipulability를 최대로 만드는 dual trajectory를 생성한다. 기본적으로 Planar Mobile Manipulation(평면에서 작용하는 모바일 매니퓰레이터)를 기준으로 한다.
Dual Trajectory Combined Control
EE와 모바일 플랫폼에 필요한 경로는 미리 우선순위와 하드웨어의 한계로 정해져있다.
기본적으로 경로는 우선적으로 생성 되기 때문에 아래 사진과 같이 EE와 모바일 플랫폼에 맞는 경로는 알고 있게 된다.
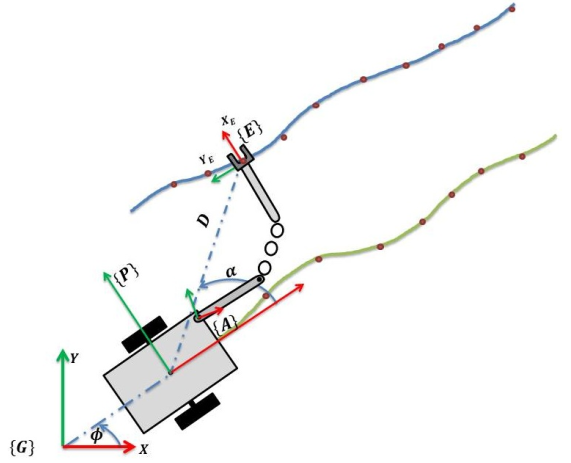
하지만, 특정 상황에서는 두개의 경로를 모두 따라갈 수 없게 되는데 이때 우선 순위가 낮은 경로에서 어느정도 타협을 통해 높은 우선순위의 경로를 따라갈 수 있게 만든다. 이런 하나의 알고리즘에서는 dual trajectory를 잘 따라가면서 다양한 Task를 수행하거나 특정 퍼포먼스를 최적화를 할 수 있게 된다.
Spherical Control Variable(D, alpha, beta)
EE는 생성 된 경로를 따라 움직이게 되고, 모바일 플랫폼은 Null space 최적화를 사용하여 EE를 따라가게 된다. 이는 실질적으로 모바일 플랫폼의 경로에 대한 완전한 제어를 제공하지는 않는데(EE에 대한 의존성이 있다는 뜻), 여기서는 변수들을 사용하여 모바일 플랫폼의 경로에 대한 직접적인 제어를 할 수 있게 한다.
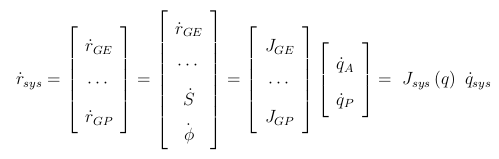
이전에 정의한 조인트 각속도에 대한 시스템들의 벡터식을 보면, 결과를 보정해주는 변수는 존재하지 않는다.
모바일 플랫폼와 EE의 모션을 수정하기 위해서 2개의 변수들이 사용된다. 이 변수들은 모바일 플랫폼의 경로와 EE 경로 간의 관계를 정의하게 되는데, D와 alpha가 된다.

D 변수는 모바일 플랫폼 중심에서 EE까지의 거리를 뜻한다.
alpha 변수는 모바일 플랫폼에서 EE위치의 XY 평면 각도를 말한다. 모바일 플랫폼에 대해서 EE의 경로를 찾기 위해서, 새번째 변수가 사용된다.
이 변수는 베타로서 수작 방향에 대한 각도로를 표현한다. 이는 EE의 Z축 좌표를 찾을 수 있게 해준다.(혹은 표현한다)
이 변수들은 모바일 플랫폼과 경로를 EE경로와의 관계로 표현하고, 모바일 플랫폼과 로봇 팔 조인트 각도와의 관계를 표현하기 위해 사용 된다. 변수 값들을 바꾸면서 최적화와 목적의 우선순위를 실행하는 모바일 플랫폼과 EE의 경로를 제어할 수 있게 된다.
변수들을 사용하는 데 가장 좋은 이점은 D 변수를 통해서 모바일 플랫폼의 EE가 얼마나 모바일 플랫폼으로부터 뻗을 수 있는 지에 대한 제한을 정할 수 있게 된다는 것이다. 즉 싱귤러에 걸리는 상황을 막아줄 수 있게 되고, 모바일 플랫폼이 좁은 공간을 이동할 때 로봇 팔의 작업공간을 제한할 수도 있다.
EE위치에 따른 모바일 플랫폼의 Pose
모바일 플랫폼은 2자유도가 존재하기 때문에 2개의 변수로 완전히 제어할 수 있다. 두개의 변수는 D와 alpha가 되고 식은 로봇 팔과 모바일 플랫폼의 조인트 각도가 된다.

위식에서 D와 알파를 추가하여 새로운 제약 조건을 추가한 식을 정리하면
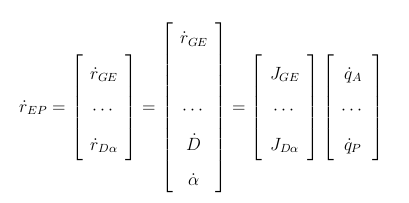
위와 같은 식 형태가 된다. 이 식을 조금 더 정리하여 E2P = Platform pose relative to EE poses 의 형태로 표현하여 보자.

이때 Task 속도 벡터에 대한 경우는 P2E로 End Effector pose relative to mobile platform poses를 이용하여 표현할 수 있다,
EE 경로는 기본적으로 6개의 변수를 가지고 있기 때문에 모바일 플랫폼의 경로에 대한 EE 경로를 표현하기에는 더 많은 변수가 필요하다. 단순히 3개의 변수만 사용하게 되면 모바일 플랫폼 Pose에 대한 EE의 위치만 표현 가능하다. Orientation에 대한 표현이 필요하다면, 그에 맞는 자코비안이 같이 사용되어야 한다(당연하게도)

이전 식들과는 조금 다르게, Orientation(w)에 관한 자코비안도 있고, 3개의 Sperical 변수들이 있다, 이 변수들이 모바일 플랫폼 Pose에 대한 End Effector의 position을 표현하는데 사용된다.
'미니멀공대생 > Control' 카테고리의 다른 글
| Mobile Manipulator 101 :: planar mobile manipulation(1) (0) | 2022.10.19 |
|---|---|
| Mobile Manipulator 101 :: Dual Trajectory & task priority(2) (0) | 2022.10.17 |
| [논문리뷰] A fast, iterative solver for the Inverse Kinematcis Problem (0) | 2022.10.10 |
| Mobile Manipulator 101 :: Pseudo-Inverse and Singularity-Robust Inverse (0) | 2022.10.05 |
| Mobile manipulator 101 :: Combined Jacobian & Dual trajectory (0) | 2022.10.03 |
