티스토리 뷰
참고한 모든 Paper는 아래 링크에 있습니다. 도움이 되셨다면 Star를 눌러주세요 ㅎ
GitHub - benthebear93/awesome-mobile-manipulator: Reading List and related repos for mobile manipulator
Reading List and related repos for mobile manipulator - GitHub - benthebear93/awesome-mobile-manipulator: Reading List and related repos for mobile manipulator
github.com
해당 글은 아래 논문을 정리한 내용입니다.
참고 논문 : Kinematic Control of Redundant Mobile Manipulators by Mashali, Mustafa
기본적으로 모바일 로봇에서는 Holonomic Constraint와 Non-Holonomic Constraint의 형태가 있다.
이에 대해서 조금 디테일 하게 이야기하자면,
로봇 시스템이 가지는 구속 조건이 무엇이냐에 따라 홀로노믹, 비홀로노믹 구속으로 나뉜다.
홀로노믹 구속은 위치와 시간만 가지는 형태이다.
간단하게는 로봇 팔과 같은 것들이 Holonomic System이다. 특징은 구속이 되어 있고,
시스템이 특정 상황으로 돌아온다는 것이다.
이와 맞게, 로봇의 자유도와 제어할 수 있는 자유도과 동일하다면 홀로노믹 시스템이라고 한다.
모바일 로봇이 옴니휠이나, 캐스터가 달려 있다면 홀로노믹 시스템이다.
반대로 Non-holonomic system이란
비홀로노믹 시스템이란 컨트롤 가능한 자유도가 실제 자유도보다 적은 시스템을 말한다.
기본적으로 자동차 같은 시스템을 말한다. 자동차는 3자유도를 가지고 있는 데 바퀴 자유도는 2개만 있다.
다수의 모바일 매니퓰레이터가 Non-holonomic 형태의 모바일과 매니퓰레이터가 합쳐진 형태이다.
기본적으로 n 자유도의 로봇 팔과 differential driven 형태의 모바일 플랫폼이 합쳐진다. 최종적으로 n+2 자유도를 가지게 된다.
Configuration은 로봇팔의 조인트와 모바일 로봇의 x, y, theta 값이 된다.
비홀로노믹 시스템이기 때문에 Kinematic model의 모바일 플랫폼은
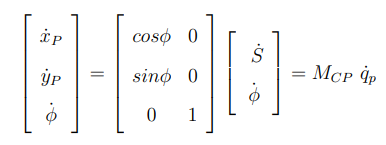
입력값으로는 linear와 angular velocity가 들어간다.
Mcp는 Cartesian 속도와 Polar 속도랑 관련이 있는 자코비안이다.
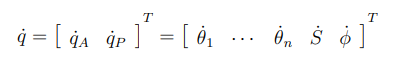
입력 속도는 아래와 같이 표현할 수 있다.
end effector의 task vector의 경우 아래와 같은 자코비안의 형태로 나타날 수 있다. GE = Ground(Global) to End effector
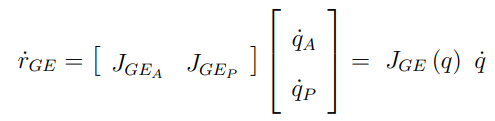
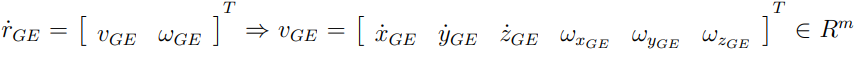
자코비안의 경우 Arm 조인트 속도 벡터에 대한 형태이고 mobile platform 조인트 속도 벡터에 대한 형태이다.
모바일 매니퓰레이터에 대한 여자유도를 이용한 알고리즘의 경우 컨트롤러를 2가지 space에서 디자인할 수 있게 해준다. Operational space와 null space. null space 공간에서는 end-effector의 상태를 변화시키지 않고 특정 상황을 최적화 할 수 있게 조정하는 프로세스가 디자인 된다. 이런 접근들은 end-effector 위치에 대한 직접적인 제어가 이뤄지지만 platform 위치(pose)는 null space 공간에서 최적화를 통해 간접적으로 제어 된다.
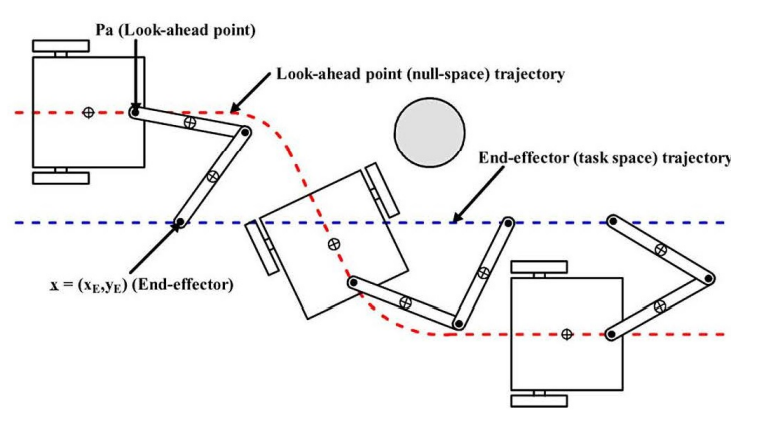
예를 들어서 end-effecor가 특정 trajectory를 따라가기 위해서는 task vector에 제약조건을 넣어줘야한다.
논문에서 말하는 mobile platform의 trajectory는 단순히 mobile platform의 2자유도를 추가하는 걸로 task vector에 추가 될 수 있다.
2자유도라 하면 platform의 translation과 rotation 속도를 말한다.
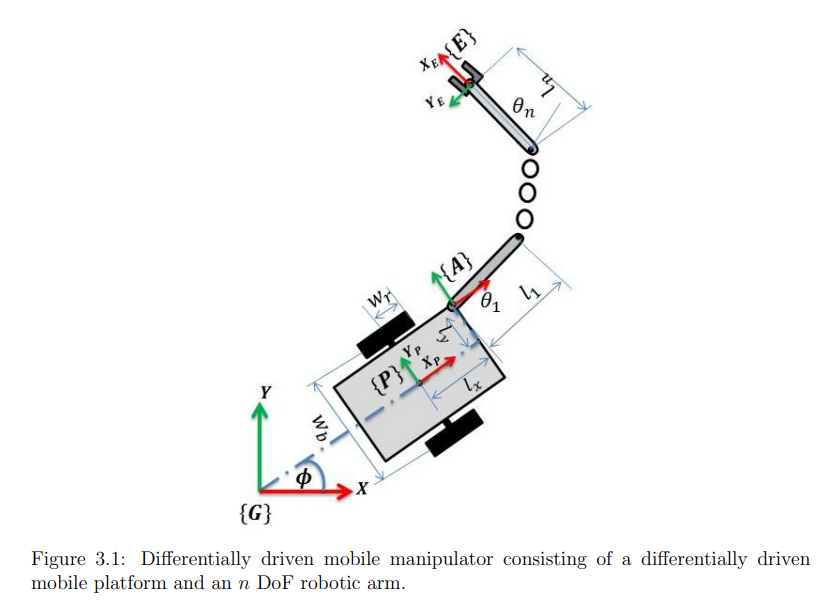
따라서 기존 r_ge 식이 r_gp로 바뀌면서 아래와 같이 된다.
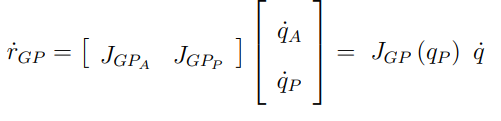
이때 arm의 조인트 속도는 mobile platform 속도에 영향을 끼치지 못하기 때문에 (실제로는 그렇지 않지만) 자코비안 중 하나는 0이 된다.
Extended Jacobian을 사용하여 Global과 End effector의 식을 End effector와 platform의 식을 정리하면 아래와 같다.
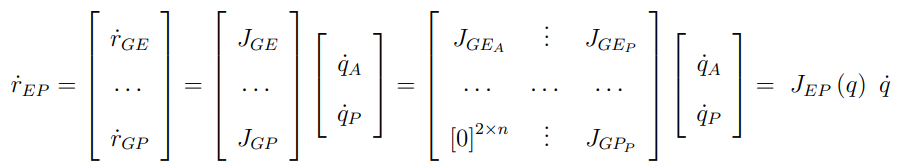
r_ep는 mobile manipulator의 desired Cartesian velocity 벡터다. J_ep가 결국 dual trajectory tracking control을 위한 자코비안 행렬이 된다. 식을 쉽게 정리하면 아래와 같다.
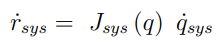
앞서 말한 것 처럼 로봇 팔의 조인트 속도는 모바일 플랫폼 속도에 영향을 주지 않는다. 또한 r_gp의 경우 직접적으로 모바일 플랫폼의 선속도와 각속도랑 관련이 있기 때문에 이에 대한 자코비안은 단위행렬이 된다. 따라서 식을 조금 더 풀어서 작성해보면
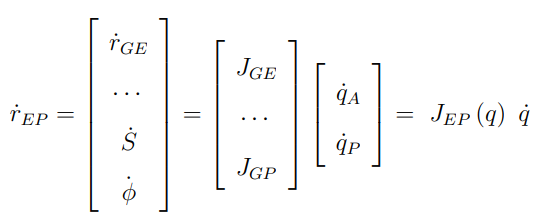
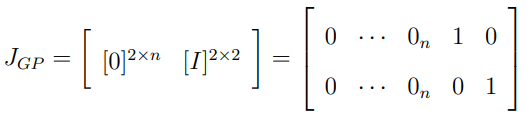
의 형태가 된다.
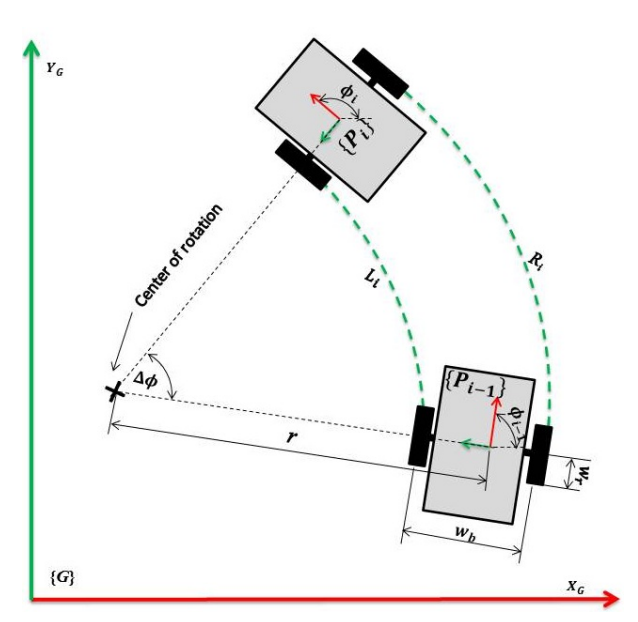
모바일 플랫폼의 경우 바퀴의 이동거리를 통해 식을 정리하게 된다.
기본적으로 Task space에서 표현하게 되지만, 위에서 언급한 것 처럼 linear, angular motion으로 표현할 수 있다.
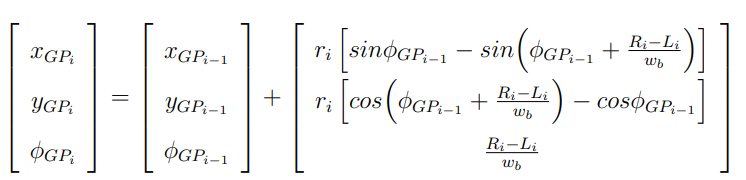
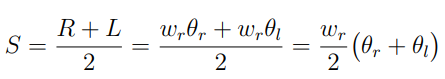
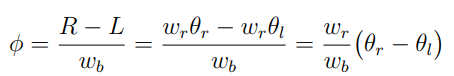
시간에 대해서 미분하게 되면 바퀴의 속도에 따른 모바일 플랫폼의 linear, angular 속도를 나타낼 수 있다.
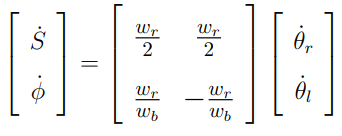
최종적으로 Global frame 기준으로 바퀴 속도에 따른 모바일 플랫폼의 Task 벡터의 식을 정리하면 아래와 같다.
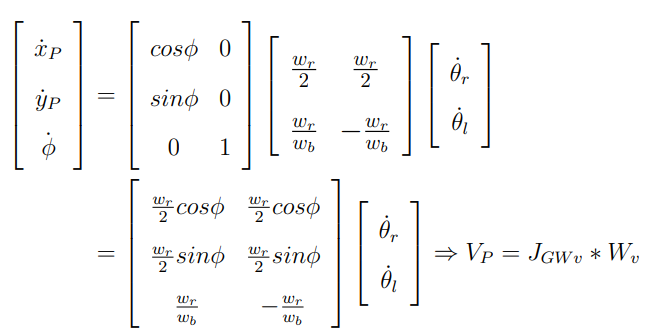
모바일 플랫폼과 로봇팔 관계
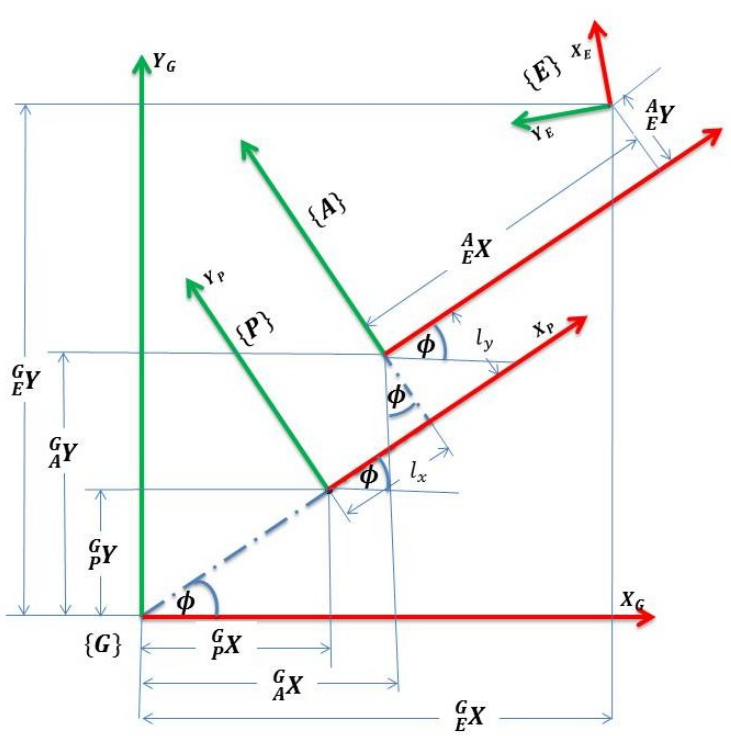
모바일 플랫폼에 대한 로봇 팔의 관계를 표현하기 위해 플랫폼과 로봇 팔의 Base의 방향이 동일하다고 하자. 그렇게 되면 둘 사이의 변환 행렬을 아래와 같이 표현할 수 있고, 이를 통해 Global frame에 대한 로봇팔 Base 식을 표현할 수 있다.
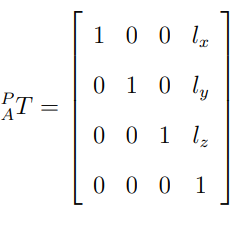
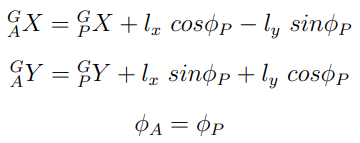
이를 동일하게 시간에 대해 미분하게 되면
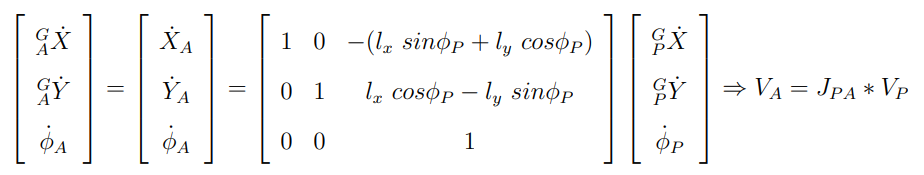
여기서 J_pa의 경우 모바일 플랫폼과 로봇 팔 Base 속도에 대한 관계를 표현한다. 이때 Global frame에 대한 모바일 플랫폼 자코비안을 사용하면 Global frame 기준에서 로봇 팔 Base의 속도를 표현할 수 있다.
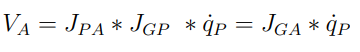
이 식에서 EE의 Cartesian 속도 식으로 변경할 필요가 있다.

단, 위 식을 모바일 플랫폼이 로봇 팔의 속도에 영향을 주는 경우를 말하는 것이지, 로봇팔과 모바일 플랫폼이 동시에 움직이고 있는 경우는 아니다.
최종적으로 식은
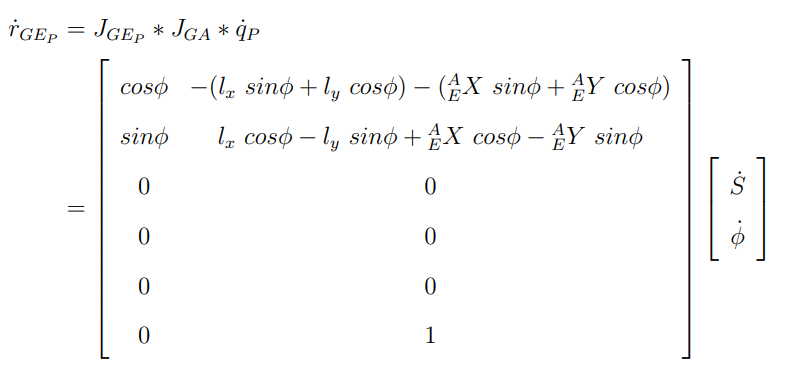
즉, 로봇 팔 ee의 속도는 2가지의 경우로 나눠서 생각할 수 있다.
1. 모바일 플랫폼은 정지해 있고, 로봇 팔이 움직이는 경우
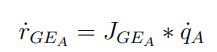
2. 로봇 팔은 가만히 있고 모바일 플랫폼만 움직이는 경우