티스토리 뷰
MIT 6.800/6.843 Robotics Manipulation :: Basic Pick and Place Part1
미니멀공대생 2022. 6. 21. 22:05작성자 : 이해구
Lecture Studty node list
- Lecture 0 : MIT 6.800/6.843 Robotics Manipulation :: Introduction
- Lecture 1 : MIT 6.800/6.843 Robotics Manipulation :: Motion planning(1)
Lecture note : https://manipulation.csail.mit.edu/pick.html
Drake 교수님은 Notation에 대한 중요성을 이야기한다. 개인적으로 나도 Notation 때문에 혹은 Orientation representation의 다양성 때문에 삽질해본 게 한두번은 아니다보니 중요성을 공감할 수 있었다. 교수님은 Drake를 만들면서 구축한 문서를 제공해준다.
Multobody Terminology and Notation
https://drake.mit.edu/doxygen_cxx/group__multibody__notation.html
위 페이지에서는 수학적으로 표기 된 Multibody를 좋은 코드로 작성하기 위해서 필요한 terminology, notation, abstraction들을 설명한다.
- 좋은 추상적인 내용 정리는 좋은 코드로 이어진다.
- Translation과 rotation을 따로 취급하면 공간 알고리즘을 제대로 추론할 수 없다.
- 표기법을 정해야 좌표 프레임에서의 에러를 막을 수 있다.
- 코드로 구현 된 알고리즘은 참고 한 문서에서 나오는 수식과 한줄 한줄 매칭되도록 짜여야 한다.
- We need a shared, unambiguous notation in code that can employ programmers' awesome pattern-matching skills to make errors visible.
(잘 이해가 안가는 부분이다)
Monogram Notation
기하학에서 가장 근본적인 컨셉은 포인트(point)이다. 포인트들은 공간상에서 일정 영역을 차지하고 있고 각각 아래와 같은 표기로 이름이 있을 수 있다.
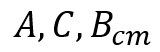
Bcm의 경우 특정 물체 B의 질량중심(center of mass)가 될 수 있다.
특정 포인트의 위치의 경우 위치 벡터로 표현한다. 이때 위치 (Position)의 p를 사용하여 아래와 같이 표현한다. (point의 p가 아니다)

position이란 상대적인 표현이다. 위치를 표현할 때는 무조건 2개의 포인트를 이용하여 한개의 위치를 다른 한 점을 기준으로 표현해야 한다. 기준되는 포인트를 왼쪽에 적어두는데, 나중에 포인트를 회전시키거나 할 때 도움이 된다.
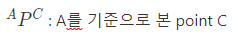
우리가 사용하는 모든 좌표계는 오른손 법칙에 의한 수직을 이루는 단위 벡터들이다. 좌표계는 모두 명확히 해야하고, express in, 한국말로 하면 '이 좌표계' 혹은 '표현 된 좌표계'라고 할 수 있는 건 더욱 중요하게 봐야한다.
"좌표계 F에 표현되어 있고 A 포인트에 상대적인 C 포인트의 위치" 는 아래와 같이 표현된다.
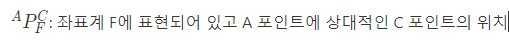
Drake 교수님은 위와 같은 position vector 에서 x 좌표만 표현하고 싶을 때는 아래와 같이 표현한다고 한다.

World frame의 경우 W로 표기하게 된다. Drake에서는 Vehicle coordinate을 World frame으로 사용한다. 정면으로 양수 x, 왼쪽으로 양수 y, 위로 양수 z 이다. 주로 사용하는 다른 좌표계는 body frame이다. Multybody system에 존재하는 모든 body들은 각각의 좌표계를 가지고 있다. Bi로 표기한다. (i번 Body)
좌표계가 가지고 있는 점과 오리진 좌표계가 일치한다면, World 좌표계에 표현되어 있고 World 좌표계에 상대적인 A 포인트의 위치는 아래 사진과 같이 쓸 수 있다.

표현이 조금 복잡하니깐 이 부분은 줄여서 표현할 수 있다. 표현을 한 사진으로 요약하자면 아래 사진과 같다.

좌표계는 방향(회전)도 가지고 있다. R로 표현하고 좌표계 표현도 동일하게 진행한다. 다만, 순수한 방향(회전) 자체는 expressed in (표현 된 좌표계)라는 게 없다는 점 참고하자.
하나의 좌표계 F 는 다른 좌표계에 대한 하나의 position과 rotation으로 완벽히 표현될 수 있다. 둘을 합쳐서 spatial pose 혹은 pose 라고 부른다. Drake 에서는 Pose와 Transform을 표현하기 위해서 RigidTransform 을 사용한다. Pose에서는 expressed in (표현 된 좌표계)는 사용하지 않는다.
Drake에서는 좌표계 표현을 코드에서 어떻게 사용할지에 대해서도 언급한다.
Pick and Place via spatial transforms
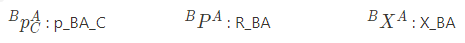
물체의 경우 O로 표기한다. 그리퍼는 G로 표기하기로 하자.이상적인 센서는 world 좌표계에서 물체(O)의 좌표계를 알려준다. 결국 Object의 좌표계와 원하는 Object의 측정 좌표계를 일치시켜주는 게 Pick and place의 기초가 된다.
물체를 Pick and place 하는 건 아래 순서와 같다.
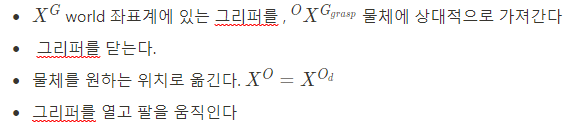
Forward Kinematics
FK의 기본적인 목적은 Joint position 값을 pose 값으로 mapping하는 것이다. (쉽게 생각해서 그리퍼 좌표계로 mapping하는 것)
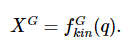
The Kinematic tree
키네마틱과 멀티바디 계산을 이용하기 위해서 MultibodtyPlant 클래스를 이용한다. 하나의 트리 구조안에 모든 바디들을 구성한다. 모든 바디들은 부모가 있고, 서로 Joint나 floating base로 연결되어 있다. vector q로 자식 조인트 좌표계로부터 부모 조인트 좌표계로의 변환을 계산할 수 있다.

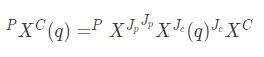
이 행렬들을 이용해 어떤 body와 부모 간의 configuration transform을 계산할 수 있다.
여기서 한가지 알아가면 좋은 것은, Joint 자체는 body간에 제약 조건이라는 것이다.즉 Joint를 만든 다는 것은 뭔가 자유도를 하나 추가한다고 생각할 수 있지만 사실은 body들 간에 제약 조건을 만든다는 것이다.
'미니멀공대생 > Control' 카테고리의 다른 글
| [논문리뷰] Robot Sensor Calibration : Solving AX=XB on the Euclidean Group (4) | 2022.07.23 |
|---|---|
| MIT 6.800/6.843 Robotics Manipulation :: Introduction (1) | 2022.06.21 |
| MIT 6.800/6.843 Robotics Manipulation :: Motion planning(1) (1) | 2022.04.27 |
| [논문리뷰] Momentum Observer-Based Collision Detection Using LSTM for Model Uncertainty Learning (3) | 2022.04.24 |
| Manipulator Compliance와 Force control에 대하여 (3) | 2022.02.08 |


