티스토리 뷰
MIT 6.800/6.843 Robotics Manipulation :: Motion planning(1)
미니멀공대생 2022. 4. 27. 22:54
#모션플래닝 #로봇 #연구 #공부 #로봇공학
Motion planning optimization-based
Motion planning이 거창해 보일 수는 있지만, 단순히 로봇팔의 초기 자세에서 differential IK를 풀어서 물체에 다가가는 것도 하나의 Motion planning이 될 수 있다. (물론 손으로 직접 작성한 Motion planning이지만) 다만, 이렇게 하지 못하는 이유는 주변 환경이 더욱 복잡해지고, 제약이 많아지기 때문이다. 인식에 대한 고려도 해야겠지만, 로봇이 Plan 할 수 있는 것도 고려해야 된다.
이번 수업에서는 Planning trajectory, 로봇 팔의 경우 조인트 q 값에 대한 Trajectory를 구하는 방식들에 대해 이야기 해보려 한다. 다양한 MP 방식들이 있지만, 실제로는 IK를 더욱 자세히 아는 것이 MP의 기초가 된다.
단계적으로
- Rich Inverse Kinematics
- Configuration space constraints
- Trajectory Parameterizations
- Kinematic Trajectory Optimization
4가지가 존재하게 되는데, 2가지만 자세히 설정하게 되면, 나머지 2가지는 자연스럽게 따라오게 된다. 결국 당연하게도 MP를 하기 위해서는 Kinematic level에서 무엇이 가능하고, 무엇이 불가능한지에 대해 알아야 한다.
Inverse Kinematics
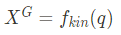
Forward Kinematics가 조인트 각도를 받아 End Effector(EE)를 뱉는 함수라면, IK는 반대로 q 를 뱉는 함수이다.
한가지 알아야할 점은, 이때 Solution은 unique 할 수도, 없을 수도 ,무한할 수도 있다.
일반적인 6자유도의 로봇의 경우 특정 상황에서 유한한 솔루션을 가지고 있고 closed form solution으로 얻을 수 있다.
geometric한 식은 sin과 cos으로 이루어져 있는데, polynomial한 식 형태로 바꿀 수도 있다.
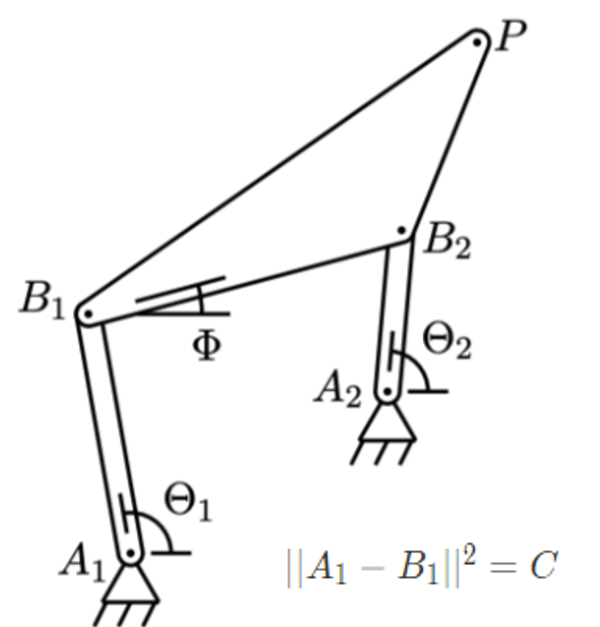
polynomial한 식으로 나타낼 수 있는 이유는 링크가 Rigid body의 형태이고, 각 axis의 점 사이의 거리의 절대값을 constrain된 값을 유지하는 형태이기 때문이다. 또한 Link1 과 Link2는 시작부분과 끝 부분을 공유하기 때문에, 이를 이용해 링크들이 연결 된 Polynomial 형태의 식을 만들 수 있다.
(물론 Polynomial을 구성하는 방법에 대한 공부를 할 필요는 없다. 왜냐? IKFast를 받아서 쓰면되니깐 ㅎㅎ..)
Generalize optimization formulations

조인트 q를 찾을 때 걸 수 있는 Constriants는 다양하다. 단순히 Elbow up, down이냐 부터, 카메라가 볼 수 있는 곳에 팔을 위치하기 위한 gaze constraints도 존재할 수 있다. 일반적으로 inequality constraint들이다. Drake 라이브러리에 가면 다양한 제약조건들을 확인할 수 있다.
IK 또한 Constrained optimization 문제로 볼 수 있다. 특히 differential inverse kinematics로 joint limit이나 joint velocity, singular avoidance, collision avoidance constriant들을 걸 고 문제를 풀 수 있었다. 다만, diff IK의 문제는 작은 q값 변화에 대해서만 (nomial configuration) 제약조건을 고려하게 된다는 점이다.
이번 강의에서는 Nonlineary/ Non convex한 optimization 문제를 선형근사나 convex 근사가 아닌 직접적으로 풀려고 해본다. SNOPT 같은 비선형 최적화 Solver로 문제를 풀 수 있는데 항상 정답을 찾는 건 또 아니다.
diff IK와 Full IK는 비슷하고 실제로 diff IK 자체가 비선형 Full IK의 One-step gradient descent나 One-step SQP(Sequential quadratic programming)라고 할 수 있다. IK란 다양한 cost와 constraint를 가진 Inverse 문제라고 생각해야 한다.
philosophy for optimization(or constraints, whatever you call it)
- Keep your cost function simple
- Add the least restrtictive constraints you can tolerate
- e.g, 컵을 집을 때 orientation은 그다지 신경 안써도 되니깐, 이런 부분에서는 constraints를 풀어줘야 한다.
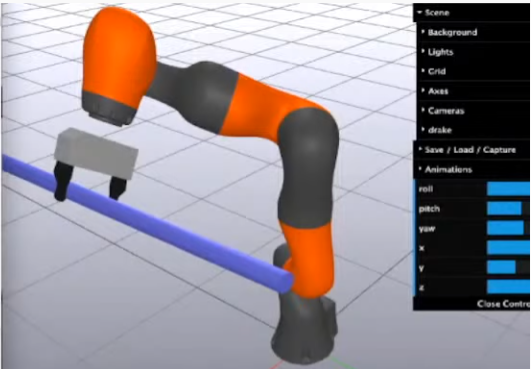
로봇 팔로 특정 실린더를 잡을 경우 그리퍼의 Orientation은 크게 영향을 미치지 않는다. 이런걸 고려해서 2가지 제약조건을 생각할 수 있다.
- 실린더 위에 포인트 A와 B가 있고, 그리퍼는 이 A와 B 안에만 있으면 된다.
- 실린더를 기준으로 그리퍼는 회전할 수 있다.
즉, 단순히 특정 위치의 실린더를 잡으라고 명령을 주는 것이 아닌, 그리퍼가 실린더 위에서만 잡고 있으면 모두 괜찮다고 명령을 주는 것이다.
제약조건을 매우 느슨하고 주어, 실린더를 더 쉽게 잡고 있을 수 있게 했다.
로봇 팔 모션에 대한 Optimizer에 대해 이야기하기 전에 Configuration space에 대해 먼저 다뤄보자.
Configuration space는 robot의 Configuration이 맞는 q(조인트 각도)의 집합이라고 볼 수 있다.
이는 두가지를 만족해야 한다.
- Joint limits 안으로 들어와야한다.
- Collision을 피해야 한다.
모션에 대한 Optimizer는 이 2개의 조건을 만족시키는 Configuration space에서 해를 찾으려고 할 것 이다.
3축 자유도를 가진 로봇 팔이 책장에 도달하는 작업을 생각해보자. 실제 grasp constraint 에 대한 해를 시각화 하게 되면 초록생 띄처럼 생긴다.
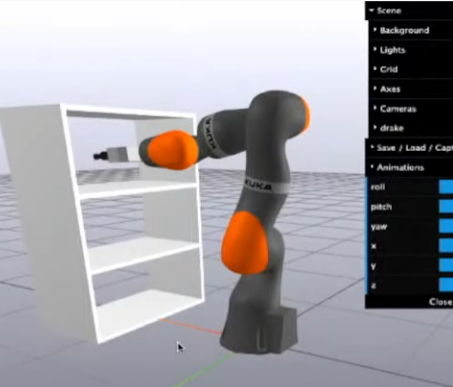

이런식의 해가 나오는 이유는 pose에 대한 제약조건이 아닌, position에 대한 constraint만 주어졌기 때문이다. 따라서 Orientation이 자유로워지면서 둥근 띠 모양의 configuration space가 나오게 된다. (제약조건이 없는 경우) (정확히 이해했는지 모르겠다..)
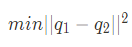
기본적인 cost function인 q변화를 최소화 하는 식과 제약조건을 추가하면 아래와 같은 사진을 확인할 수 있다.


왼쪽 사진에 이차 함수 형태를 보이는 초록색이 바로 cost function이다. 오른쪽 사진과 다른 점은 왼쪽은 local이고 오른쪽이 global로 실제
SNOPT에 들어간 constraint와 cost function C space의 전체 형태이다. 결국 제약 조건안에서 c space만 설정할 수 있다면 초기 조건을 토대로 c space안에서 연속적인 point들을 찾아가기만 하면 된다.
수업자료에 보면 언제 IK를 쓰고, 언제 diff IK를 써야할까라는 질문이 있다. 그에 대한 내용을 정리해보자.
IK는 조금 더 global 한 문제를 풀지만, 수렴을 보장하지는 않는다. 또한 제약조건과 cost function에서 작은 변화를 만들기 때문에 실제 joint q에서는 작은 값으로 바꾸지 못할 수도 있다. (크게 움직일 수도 있다는 뜻). Global한 문제를 풀 때는 IK를 쓰고, 실제 q trajectory를 생성할 때는 optimization을 추가하여 생성해야한다. 아니면 End effector space에서 부드러운 명령을 내려서 joint space에서 잘 따라가도록 할 수 있다면 diff IK를 사용하는 것도 가능하다고 한다.
kinematic trajectory optimization은 다음 글에 이어서...
'미니멀공대생 > Control' 카테고리의 다른 글
| MIT 6.800/6.843 Robotics Manipulation :: Introduction (1) | 2022.06.21 |
|---|---|
| MIT 6.800/6.843 Robotics Manipulation :: Basic Pick and Place Part1 (1) | 2022.06.21 |
| [논문리뷰] Momentum Observer-Based Collision Detection Using LSTM for Model Uncertainty Learning (3) | 2022.04.24 |
| Manipulator Compliance와 Force control에 대하여 (3) | 2022.02.08 |
| Disturbance, Momentum, State Observer에 대해서 (1) | 2022.01.30 |
