티스토리 뷰
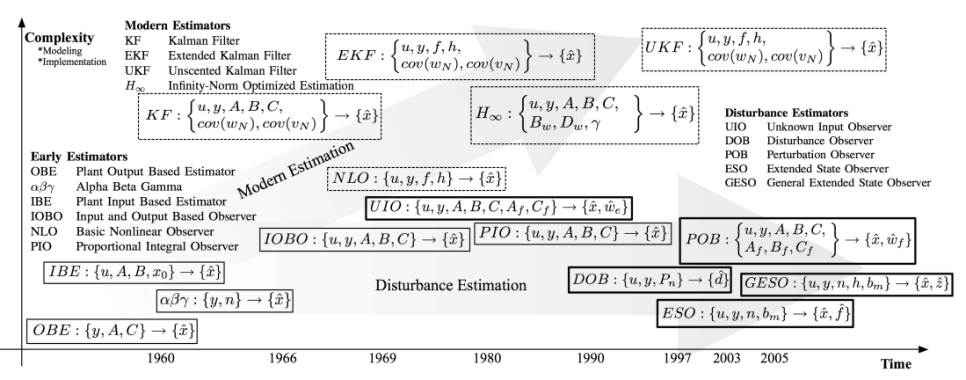
과거의 Observer부터 현대의 Observer를 설명해보려 한다. 과거의 Observer는 간단한 정의만 다루고 현대의 Observer를 자세히 설명하겠다.
1. Plant Output Based Estimator(OBE)
Plant의 결과(Output)값으로부터 정보를 관측하는 관측기이다. 이를 기준으로 한 Observer로 low pass noise filter, apporixmatic differentiator, 알파-베타-감마 필터가 있다.
2. Input and Output Based Observer(IOBO) = Luenberger Observer
OBE와 IBE를 합쳐둔 걸로, measure data를 피드백 해주는 형태의 관측기이다. 따라서 Closed loop observer라고도 부른다. 이 관측기의 이득은 노이즈를 줄이고 초기값 조건과 상관없이 phase lag 정보를 얻을 수 있다는 점이다.
3. Basic Nonlinear Observer
단순히 IOBO 형태를 비선형 모델에도 적용이 가능하도록 하게 한 관측기이다.
Disturbance Observer (DOB)
외란 관측기에 대해서 알아보자. 외란이란 일반적으로 원하는 입력이 아닌 외부에서 들어오는 외력을 뜻한다. 여기서 관측기가 하는 일은 입력과 외란이 들어간 시스템의 결과를 통해 외란을 예측하는 것이다.
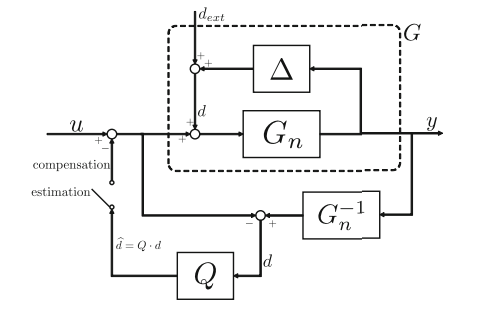

시스템 결과를 이용해서 외란을 예측하려면 가장 쉬운 방법으로는 시스템 모델의 역수를 결과에 곱해주면 된다. 다만 시스템 모델의 역수는 unrealizable 하기 때문에 실제로는 문제가 있다. (unrealizable하다라는 뜻은 전달함수의 형태가 실제 물리 환경과 매칭하는 형태가 아니라는 뜻이다.) 따라서 이를 realizable 하게 만들어주기 위해서는 low pass filter의 형태인 Q filter를 곱해준다.
Momentum based observer
다만 일반적인 DOB의 경우 이너시아 매트릭스에 대한 비선형과 커플링 효과로 인해 바로 로봇 제어 시스템에 적용하기 어렵다. (커플링이란 이너시아 행렬에 곱해지는 행렬들로 인해, 대각행렬이 아닌 형태가 되는 것을 말한다) 이를 해결하기 위해서 비선형 외란 관측기에 대한 연구도 진행되어 왔고, 이너시아의 일반적인 운동량을 제시하여 비선형성과 커플링 효과를 제거하는 연구도 진행됐다. 다만 이는 외란에 대해 완전히 모르는 상황에는 적용되기 힘들다. 이를 해소하기 위해 운동량 기반 DOB가 제시됐다. (추가적으로 운동량 기반 DOB의 형태는 residual 기반 estimator와 비슷하다 라는 것을 알고가면 좋다). 이 관측기의 특징은 3가지이다.
1. 관측기 설계와 구현이 매우 쉽다.
2. 운동량 기반 관측기의 결과는 실제 외란이 low pass filter를 거친 결과이다.
3. 관측기의 형태는 구조적으로 일반적인 DOB와 같다.
운동량 기반 관측기는 일반적으로 rigid body joint 로봇 형태에 사용되는데, 모터의 이너시와 링크 이너시아 사이의 탄성력이 고려되어야 하는 flexible joint 로봇에도 사용될 수 있다. 특히 탄성력 때문에 이너시아에 커플링 효과가 일어나 동역학식을 만들기 어려운 상황에 쓰면 좋다. 추가적으로 링크와 모터의 동역학식을 따로 고려해서 운동량 기반 관측기를 적용할 수 있다.

일반적인 로봇팔의 동역학 모델이다. 이너시아 항과 코리올리 항, 중력 항이 존재한다. 이때 코리올리 항을 이용해서 이너시아의 미분 항으로 표현할 수 있다.

이를 이용해서 로봇의 운동량 식을 정의하면 아래와 같다.

여기서 현실적으로 모델링 파라미터들에 대한 값을 정확히 알 수 없기 때문에 아래와 같이 표현해야한다. (모델링 오차가 있다는 뜻이다)

식에서 토크 항의 경우 모터 토크와 외란(disturbance)에 대한 항으로 나눠 표현할 수 있다. 여기서 나타나는 외란의 경우 마찰에 의한 토크가 될 수도, 외부에서 들어오는 토크가 될 수도 있다. 우리가 궁극적으로 하고 싶은 일은 외란 토크를 예측하는 일이다.
모터 토크를 control 토크로 두고 식을 정리하여 관측기 동역학 모델을 정리하면 아래와 같다,

일반적인 운동량식과 관측기를 거친 운동량 식 차이를 정리하면 궁극적으로 관측기를 거친 외란의 값을 알 수 있다.

이 결과는 실제 외란이 omponent-wise low pass filter를 거친 형태를 보인다. 이를 구현을 위해 정리하여 표현하면

residual-based estimator와 같은 형태라는 것을 볼 수 있다.
쭉 정리하면 아래와 같은 형태가 된다.
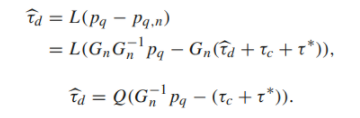
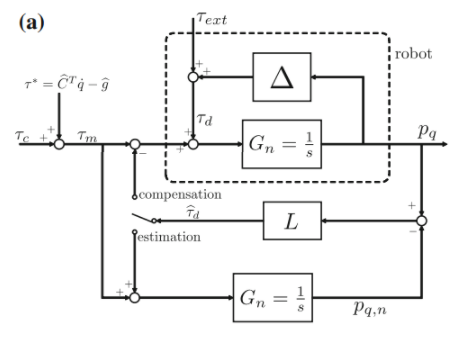
운동량 기반 관측기의 블럭선도는 아래와 같다.
State Observer
일반적인 Disturbance observer와 다른 형태의 Observer로 state observer가 있다. disturbance observer는 외란을 예측하는 것이 목적이었다면, state observer는 로봇의 상태를 예측하는 것이 목표이다. 둘 다 모델링 에러나 외란에 대한 영향과 관련이 있다는 점에서는 동일하지만 궁극적으로 구하고자 하는 것이 무엇이냐에 따라 나뉘게 된다. 추가적으로 state observer에서 중요하게 생각하는 부분은 시작 상태 (Initial state)이다. 로봇의 시작 상태를 정확히 알 수 없는 상황이 많기 때문에 이를 이겨내고 정확한 상태를 예측하는 obserever가 필요하다.

State observer 형태로 다양한 칼만필터와 H infinity filer가 존재한다,
참고자료
BACK, Juhoon; HA, Wonseok. Robust tracking of robot manipulators via momentum-based disturbance observer and passivity-based controller. International Journal of Control, Automation and Systems, 2019, 17.4: 976-985.
RADKE, Aaron; GAO, Zhiqiang. A survey of state and disturbance observers for practitioners. In: 2006 American Control Conference. IEEE, 2006. p. 6 pp.
CHEN, Wen-Hua, et al. A nonlinear disturbance observer for robotic manipulators. IEEE Transactions on industrial Electronics, 2000, 47.4: 932-938.
'미니멀공대생 > Control' 카테고리의 다른 글
| [논문리뷰] Momentum Observer-Based Collision Detection Using LSTM for Model Uncertainty Learning (3) | 2022.04.24 |
|---|---|
| Manipulator Compliance와 Force control에 대하여 (3) | 2022.02.08 |
| [Manipulator] Control (0) | 2022.01.13 |
| [Manipulator] Dynamics (2) | 2022.01.11 |
| [임피던스 제어] Improving Low-Impedance Performance (Series Dynamics) (0) | 2022.01.05 |
