티스토리 뷰
Position control
로봇 제어에 있어서 위치제어를 먼저 설명해보려 한다.
로봇 팔 끝단을 제어하는 방법으로는 Joint space에서의 제어와 Cartesian space에서의 제어가 있다.
따라서 Joint space 제어기와 Cartesian space 제어기 2개가 존재한다. 이 글에서는 각 제어기가 사용하는
PD제어기나 PID제어기를 설명해보려 한다.
Proportional derivative controller
PD제어기는 로봇 팔 끝단의 위치오차와 이의 미분 값이 속도 오차의 비례항으로 구성된다.

이는 일반적인 PD 제어기와 전혀 다를게 없다. Kp와 Kv 값에 따라서 시스템 응답이 달라지게 된다. 이들 값은 시스템의 고유진동수와 댐핑 계수에 연관이 있다.

이 두개 값은 과도구간 응답에 영향을 미치고, 2차 시스템의 응답 특성들 중 상승시간(t_rise), 오버슛 정도(M_peak), 수렴시간(t_settle) 등이 시스템 제어기를 설계할 때 사용된다. 각 응답 특성들은 고유진동수와 댐핑간의 관계를 아래와 같이 가져간다.

모델링 오차와 외란
기본적으로 앞서 언급한 내용들은 시스템이 이상적인 경우를 생각한다. 하지만 시스템의 정확한 질량값이나 명령값인 힘을 알 수는 없다. 따라서 시스템에 외란(d)이 들어온다고 하고 모델링을 고려하면 아래와 같다.


이 식을 정상상태에서 확인해보면, d = Kp(x_d - x)의 형태로 나온다. 즉 위치 오차가 정상상태에서도 0이 되지 않는 다는 것이다.

위치 오차를 줄이기 위해서는 Kp 값을 증가시켜서 줄 일 수 있다. 하지만 Kp값을 크게 증가시킬 수 없기 때문에 정상오차는 적분기를 추가하여 해결할 수 있다. 이게 PID 제어기가 된다. 사실 로봇팔에 적용한다고 해서 새로운 점은 딱히 없다.

Joint space 제어기로 아래 글에서는 독립 관절 제어기, 중력보상, 동역학을 통한 제어기 설계에 대해서 이야기 해보려한다.
독립관절 제어기란 다른 관절들이 주는 동역학적 영향을 외란으로 간주하고 하나의 관절에 대해 설계한 제어기를 말한다. 기본적인 동역학 모델은
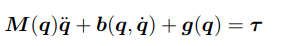
M은 관절공간의 관성행렬, b는 관절공간의 코리올리 및 구심력 벡터를 말하며, g는 관절공간에서의 중력벡터를 말한다. 6자유도의 로봇 팔일 경우 관성행렬은 6x6 행렬이 되는데, 첫번째 관절의 동역학식만 뽑으면 아래와 같다.

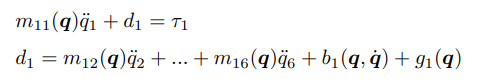
독립 관절은 다른 관절이 주는 영향을 외란으로 간주한다고 하였기 때문에 m11,q1'', d1을 관련 된 식을 빼고 다 외란으로 취급한다, 각 관절에 대한 PD 제어기를 통해 구성해주면 된다.


중력보상
일반적으로 로봇의 키네마틱스만 풀어 위치제어를 진행할 경우 중력보상에 대한 고민을 별로 하지 않는다. 하지만 실제로 동역학 모델을 기준으로 제어기를 설계할 경우 로봇 작동에 영향을 줄 수 있는 것이 중력에 대한 힘이다. 중력이 관절이나 로봇 끝단에 주는 영향은 식으로 계산할 수 있다. 이를 계산하여 각 토크에 중력에 대한 보상 값을 넣어주게 되면 더욱 정밀한 제어기 설계가 가능해진다.

g_hat의 경우 중력값을 예측한 행렬을 말한다.
중력보상 제어기 설계는 단순하다. 앞서 설명했던 PD 제어기에 중력보상 토크값만 더해주면 된다.

동역학 식에 토크를 대입하여 정리하게 되면

이때 중력에 대한 예측값이 정확하다고 하면 중력에 대한 항 g(q) = g_hat(q)가 되면서 항이 사라지게 된다. 결국 중력보상을 적용한 PD제어기는 중력에 대한 외란을 지우면서 제어기 성능을 향상 시키게 되는 것이다.
동역학 모델링에서의 중력보상을 고려한 제어기를 이야기해보자. 동역학 모델링에서는 관성 행렬, 코리올리 및 구심력 벡터, 중력벡터에 대한 값은 예측값을 사용하게 된다. 이렇게 예측한 값들을 이용해 작성한 동역학 모델은 아래와 같다. 여기서 한가지 다른점은 q''이 토크'으로 표현됐다는 것이다. 이 부분을 참고해서 식을 보자.
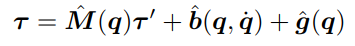
이 토크값을 일반적인 동역학 식에 적용하면

예측값들이 정확하다고 하면

이렇게 되는데, 결국 각 관절의 관성 값이 단위 질량인 시스템이 되버린다. 따라서 PD 제어기를 설계하면 아래와 같이 나온다.
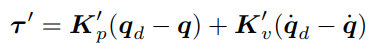
이때 토크'의 값은 각 관절의 가속도값이 되며, 이를 통해 관절을 독립적으로 제어할 수 있게 된다.
따라서 궁극적으로 제어기 식을 정리하게 되면 아래와 같다.

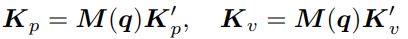
위치제어의 방법으로는 여러가지가 있다.
1. 역기구학을 이용한 위치제어
역기구학 이용한 위치제어는 로봇 끝단의 위치에 맞는 관절각도를 구하는 것으로 아래 수식으로 표현할 수 있다.

f(x)는 순기구학을 뜻하고, 이를 역으로 하여 관절 각도를 구할 수 있다.
2. 자코비안 역행렬을 이용한 위치제어
자코비안 역행렬은 끝단의 위치에 따른 관절각도를 구하는 것은 동일하지만, 역기구학이 아닌 관절과 로봇 끝단의 움직이는 정도를 이용한다.
자코비안은 끝단과 관절을 매핑하는 매핑함수이다. 끝단 속도와 관절 속도를 나타내는 식으로 표현해보면 아래와 같다.
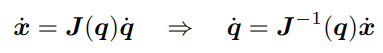
이 식에서 끝단의 움직이는 정도와 관절의 움직이는 정도를 표현하여 관절각도를 계산할 수 있다.
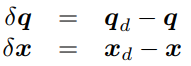
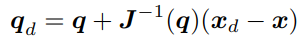
자코비안 역행렬 위치제어 방법에서 한가지 고려해야할 점은 위치와 속도 오차를 사용하기 때문에 오프라인으로 계산이 안되고 제어주기 안에서 온라인으로 진행해야 한다는 점이다. 이러한 부분이 역기구학을 이용한 제어와 다른점이다. 추가적으로 역기구학 자체는 사용되지 않기 때문에 역기구학에 대한 정보가 필요없다.
3. 자코비안 전치행렬을 이용한 위치제어
이 방법에서는 끝단위치제어를 위한 토크를 생성한다. 이때는 동역학 모델을 사용하지 않는다.
끝단에서 도달해야할 위치로 힘을 가해서 위치제어를 하게 된다. 이는 힘-토크 매핑 자코비안을 이용하여 표현이 가능하다.

이때 힘은 PD 제어기를 사용하여 만들 수 있는데, 위치오차와 속도오차를 이용하여 표현할 수 있다.

한가지 참조할 점은 위치오차 항은 위치 방향으로 힘을 만들지만, 속도오차 항은 그렇지 않을 수도 있다.
PD항에 대한 값은 사양에 맞게 계산하면 된다.
Position control with operational space dynamics
Joint space에서의 위치제어와 동일하게 동역학 부분을 고려하면 된다. 일반적으로 우리가 원하는 좌표 방향들의 동적 연결을 동역학식을 이용해 보상하여 원하는 형태로 제어하고자 함이다. 결과적으로 우리는 목표 위치로의 움직임을 만들어 내고 싶은데, 이에 필요한 힘의 방향은 목표위치와는 다를 수 있다. 설계할 제어기는 관성 행렬을 고려하여 제작된다.

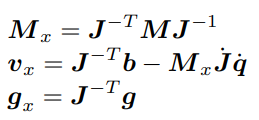
위 식들은 라그랑주 운동 방정식으로 유도될 수 있다.
운동에너지를 고려해보면 아래와 같고

위치에너지의 미분 값은 아래와 같다.

이를 정리하면 아래처럼 표현될 수 있다.

위에서 언급한 동역학 식을 이용해 작업 공간에서 위치 제어기를 설계하면 된다. 작업 공간에서의 f를 동역학 예측값과 PD제어기를 사용한다.

동역학 행렬들의 예측치가 같으면 작업공간에서의 위치제어는 단위질량 (1)에 대한 PD 제어기가 된다. 이때 각 PD값을 조인트마다 다르게 설정함으로서 방향 운동이나 회전 운동에 대한 독립적인 제어기를 만들 수 있다. 실제 Kp'와 Kv'값은 아래와 같기 때문이다.

동역학 위치제어기가 왜 필요한지 모를 수 있는데, 실제 각 관절에 대한 PD 값을 조절함으로서 특정 관절 속도가 다른 관절 속도보다 느리거나 빠른 형태의 제어를 할 수 있다. 이런 점들은 역기구학이나 자코비안 역행렬 방식으로는 구현할 수 없는 특징이다.

'미니멀공대생 > Control' 카테고리의 다른 글
| Manipulator Compliance와 Force control에 대하여 (3) | 2022.02.08 |
|---|---|
| Disturbance, Momentum, State Observer에 대해서 (1) | 2022.01.30 |
| [Manipulator] Dynamics (2) | 2022.01.11 |
| [임피던스 제어] Improving Low-Impedance Performance (Series Dynamics) (0) | 2022.01.05 |
| [임피던스 제어] Improving Low-Impedance Performance (2) | 2021.12.24 |
