티스토리 뷰
로봇 팔 다이나믹스에 대한 이해가 좀 떨어지는 것 같아서 조금 정리해보려고 한다.
라그랑주 운동방정식 (Lagrange equation of motion)
라그랑주 운동방정식은 Minimal principle을 기준으로 정의되는데, 로봇 팔에서는 각 관절에 따른 운동 변수와 관절 모터의 토크를 이용해 라그랑주 방정식이 정의된다.

라그랑주 운동방정식은 토크와 운동방정식, 위치에너지의 관계를 말한다. 식에서 L은 라그랑지안으로 운동에너지와 위치에너지의 차이로 정의 된다. 즉 토크는 운동에너지와 위치에너지의 차이를 각위치(각도)와 각속도 기준으로 편미분 한 식들과 관계가 있다는 뜻이다.
다관절 로봇의 운동에너지는 일반운동에너지랑 별 차이가 없다.
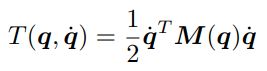
M(q)는 이너시아 매트릭스이다. 운동에너지 식 T(q, q')을 이용해서 라그랑주 운동방정식을 새롭게 정의하면 아래와 같다.

이 식을 조금 깔끔하게 정리하면 자주 본 로봇 동역학 식이 나온다.

g(q)의 경우 위치에너지로서 중력벡터를 뜻한다. C(q,q')q'은 코리올리 벡터/구심력 벡터를 의미한다. 코리올리 벡터항은 아래와 같이 표현된다.

위 식은 코리올리 항은 각속도의 2차 방정식 혹은 2차 벡터식의 형태가 되는 것을 알 수 있다. 이를 2차원/ 3차원 텐서 기호를 사용하기 위해서 코리올리 행렬 C(q,q')의 요소들을 2차원 텐서로 표현한 식 C_ij는 아래와 같다.


여기서 c_ijk는 3차원 텐서로 크리스토펠 심불이라고 부른다. 3차원 텐서를 이용해 M-2C(q,q') 값이 skew symmetric 행렬이라는 것을 보일 때 사용될 수 있다.
One DOF Manipulator dynamic model
위에서 언급한 라그랑주 운동방정식을 이용해서 1 자유도의 동역학 모델을 만들어보자.

Point mass
끝부분에만 질량이 있는 로봇을 생각해보자. 속도는 lq'으로 운동에너지와 위치 에너지를 계산해보면 아래와 같다.


라그랑지안을 구해서 동역학 모델을 구해보면 아래와 같다,
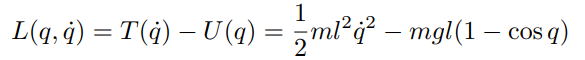

Link inertia
만약 끝부분에만 질량이 있는게 아니라 정말 로봇팔과 같은 사각형 형태의 팔일 경우에는 링크의 이너시아를 고려해야한다.

위치에너지의 경우 별 차이는 없지만 링크 중심거리 r를 고려해야하기 때문에
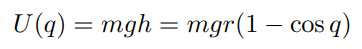
라그랑지안과 이를 이용해 동역학 모델을 구하면 아래와 같다.


Two DOF Manipulator dynamic model
따로 점질량 문제는 풀지 않고 바로 링크들에 대한 관성이 있는 경우에 대해 알아보자.
Link inertia

1 자유도 로봇 팔과 동일하게 2자유도 로봇 팔도 가장먼저 속도를 계산하고, 이를 이용해 운동에너지를 계산해주면 된다.
첫번째 링크의 속도는 바로 구해지는데, 2번째 링크는 각 링크(1번,2번 모터)의 속도와 자체 링크의 속도의 백터 합성을 통해 얻어진다.
회전속도도 동일하게, q1'과 q1'+q2'으로 계산할 수 있다.
이에 대한 운동에너지와 위치에너지를 계산한다.
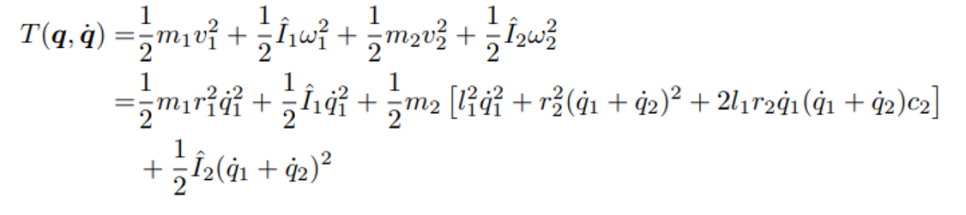
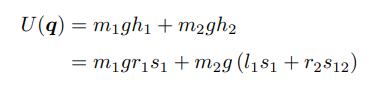
이를 이용해서 라그랑지안 함수를 만들어 계산하면 동역학 모델을 계산할 수 있다.
뉴턴-오일러 운동방정식 (Newton Euler )
뉴턴 오일러 방법은 global 좌표계로 부터 End effector 좌표계까지 좌표계를 이동시키면서 속도를 계산하고 다시 End effector에서 global 좌표계로 돌아오면서 힘/모멘트를 계산하는 방식으로 진행된다. 이를 Forward recursion/ Backward recursion 이라고 부른다.
Forward Recursion
FR은 쉽게말해서, 이전 링크의 속도(직진, 회전)를 이용해서 현재 링크의 속도(직진, 회전)을 계산하는 방법을 말한다.

식을 조금 음미해보자면, 현재 링크(i)의 직진속도는 이전링크의 직진속도와, 회전속도를 더하고, 관절 운동이 가능한 방향 벡터값을 더해줘서 직진속도를 계산한다. 관절 운동 방향 벡터는 주로 z축이기 때문에 [0, 0, 1]로 설정되고, 제타는 revolute냐 prismatic이냐에 따라 달라진다. 가속도는 당연하게도 미분해주면 된다. 단 외적 미분은 조심해야되는 부분이니 미분한 결과를 보고 가자.

Backward Recursion
BR은 힘과 모멘트를 직진 운동과 회전 운동 사이의 관계식을 얻는 방법이다.

링크의 무게중심인 부분에서의 직진속도를 구하면 아래와 같다.

힘에 대한 식을 정리하면 아래와 같다.

한가지 고려해야할 점은, 다음 링크에서 오는 반작용힘이다. f_i+1로 표시되어 있는 데, 이 부분을 놓칠 수 있기 때문에 참고하자.
p_ci' (링크의 직진속도)를 미분하여 가속도를 구할 수 있고, 이는

이 식들을 이용해서 현재링크의 운동 방정식을 구하면
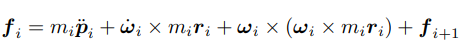
힘뿐만 아니라 모멘트도 구해야 한다. 전체 모멘트와 관성 모멘트가 같다는 걸 사용하면 된다.
관성모멘트를 계산하는 게 조금 까다로울 수 있다. 책에서는 링크 관성 평행이동을 사용한다. (스테이너의 정리)
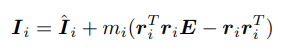

여기서 구한 힘과 모멘트 통해 모터에 필요한 토크를 실제 관절 구동 방향 벡터로 projection 시켜 계산해야한다. 추가적으로 고려해야될 사항들은 모터의 관성과 관절의 마찰력등이 있다.
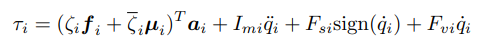
motor inertia의 약자로 mi는 모터 자체의 관성 모멘트이며, si는 stiction의 약자로 정지 마찰계수를 말한다. vi는 왜인지 모르겠지만
관절의 클롱 마찰계수를 말한다. sign은 q'의 값에 따라 1, 0, -1로 바뀐다.
정리1
라그랑주 방식과 뉴턴 오일러 방식을 통해 동역학 모델을 알아봤다. 라그랑주 방식은 에너지에 대한 미분을 통해 힘을 구한다는 점이며 뉴턴 오일러 방식은 단순히 대수학만을 이용해 계산된다는 점이다. 실제 프로그래밍으로 동역학 모델을 구현할 때는 대수학만 사용하는 뉴턴 오일러 방식이 더 쉽다고 한다. 이부분은 추후에 구현하여 정리해보겠다.
Forward/Direct dynamics
순기구학이랑 동일한데, 단순히 힘/토크로 바꿔 생각하면 된다. 입력값으로 힘/토크가 들어가면 그에 따른 관절의 가속도를 계산하는 작업이다.
Inverse dynamics
역동역학은 역기구학이랑 동일하다. 주어진 가속도 정보로 관절의 힘/토크를 계산하는 것이다.

기본적인 동역학 모델을 조금 더 수정해서 보면
비선형 토크를 아래와 같이 표현해서 볼 수 있다.


f_ext는 external의 약자로, 외부에서 로봇으로 들어오는 힘/모멘트 값을 말한다. 역동역학을 통해 관성 행렬과 비선형 토크를 계산하는 것이 목표이다. 이는 라그랑주나 뉴턴 오일러 방식을 통해 구할 수 있다.
가속도 q''을 계산은 위 식에서 관성행렬을 단순히 역행렬하면 된다.
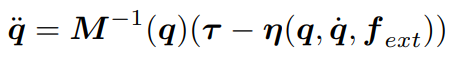
위 식을 각속도와 각가속도로 나눠 행렬을 정리하면 미분 방정식 형태로 나타낼 수 있게 된다.

미분 방정식의 형태로 식을 정리했으므로, 수치 근사를 사용하여 해를 구할 수 있다. 수치 근사 방법으로는 오일러 적분이나 룬게쿠타 방식들이 있다. 오일러 방식의 오차를 줄이기 위해 사용되는 방법이 룬게쿠타
오일러 방식
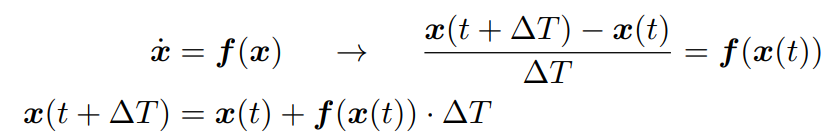
룬게쿠타 방식

동역학 파라미터에 대한 선형 동역학
당연하게도 실제 로봇에서 동역학 모델을 사용할 경우에, 로봇의 무게, 거리, 관성, 마찰계수 등을 모른다. 동역학 모델을 이용해서 동역학 파라미터들을 추정할 수 있다. 동역학 모델 식을 정리해보자.
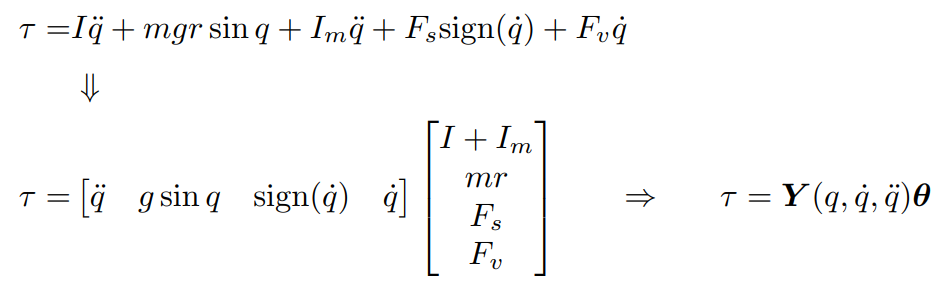
I와 Im은 링크 관성과 구동기 관성이며, m은 질량, r은 원점과 무게중심 사이의 거리, Fs는 정지마찰계수, Fv는 운동마찰계수이다. 즉 동역학 파라미터들의 집합이다. 이때 Y(q,q',q'')은 regressor라고 불리는 벡터로 위치, 속도, 가속도를 통해 표현된다. 리그레서는 비선형적인 동역학 모델 식을 선형적으로 보이기 만들어 줄 수 있다.
일반적으로 4개의 입출력 데이터를 통해 동역학 파라미터 벡터를 찾을 수 있다. q,q',q''과 입력 토크를 4번 실험하여 동역학 파라미터를 계산할 수 있다(미지수인 파라미터가 총 4개이기 때문에). 이를 수식으로 정의 해보면,

이 식이 유일해를 가지려면 가속도를 측정할 수 있어야하고, 리그래서 행렬의 역행렬이 존재해야 한다.
즉, 동역학 모델과 유일해 조건만 갖춰진다면, 동역학 파라미터를 식별할 수 있다.
동역학 파라미터를 식별하는 알고리즘에 대한 자세한 내용은 따로 적지 않으려고 한다.
'미니멀공대생 > Control' 카테고리의 다른 글
| Disturbance, Momentum, State Observer에 대해서 (1) | 2022.01.30 |
|---|---|
| [Manipulator] Control (0) | 2022.01.13 |
| [임피던스 제어] Improving Low-Impedance Performance (Series Dynamics) (0) | 2022.01.05 |
| [임피던스 제어] Improving Low-Impedance Performance (2) | 2021.12.24 |
| [Null space control] redundant manipulator control with optimal target function (0) | 2021.09.22 |
