티스토리 뷰
[논문리뷰] Robot Sensor Calibration : Solving AX=XB on the Euclidean Group
미니멀공대생 2022. 7. 23. 15:58Robot Sensor Calibration :
Solving AX=XB on the Euclidean Group
저자 : Frank C. Park, and Bryan J. Martin
논문 : https://ieeexplore.ieee.org/document/326576
작성 : benthebear93
구현 : https://github.com/benthebear93/Calibration_AX_XB
ABSTRACT
유클리드 군 안에 있는 AX=XB는 손목축에 올려져 있는 센서를 보정하는 문제에서 많이 사용된다. 이번 논문에서는 리 그룹 이론의 방식을 사용하여 기하학적으로 시각화 할 수 있는 해석해를 찾을 수 있는 닫힌 식(closed form exact solution)을 유도하고, 노이즈가 있는 상태에서 측정 되는 A와 B가 있는 경우의 닫힌 형태의 least square 해를 유도한다.
INTRODUCTION
손목축에 달린 센서를 켈리브레이션하기 위해서 A와 B를 알고, X를 모르는 경우를 풀어야 한다. 이때 A 행렬은 임의의 움직임 후 손목 좌표계에 대한 자기 자신(움직인 후의)의 위치(Position)와 방향(Orientation)를 뜻하고, B 행렬 또한 동일한 움직임 후의 센서 좌표계에 대한 자기 자신(움직인 후의)의 좌표계(위치와 방향)을 뜻한다. 이때 X 행렬은 손목축에 대한 센서 좌표계를 뜻한다. 보정은 임의의 움직임을 몇번 한 후 AX=XB 문제를 풀어 X 행렬을 얻어, 정확한 센서의 위치를 얻기 위함이다.
이번 논문에서는 리 그룹에서 least square를 통한 문제 해결과 닫힌 해를 찾는 방식을 보여준다.
이 방식의 장점은 유클리드 군에 대한 정준좌표계(Canonical Coordinate)의 집합이 존재한다는 것이다. 이때 유클리드 군은 AX=XB 문제에 특히 간단한 특징의 해를 만들어 준다. 이때 해는 명시적으로 표현 가능하며, 기하학적으로 시각화를 간단히 된다. (정준좌표계는 간단하게 시간에 대한 물리적 변화가 없는 좌표계를 말한다. 좀 복잡한 내용이긴 한데, 물리적 상황에서 시간이 지나도 물리적인 변화가 없다는 것이다. 센서 보정 같은 현상도 시간이 지나도 물리적인 변화가 없기 때문, 근데 솔직히 잘 모르겠다....)
센서 보정에서는 노이즈가 무조건 존재하기 때문에 측정을 여러번 거쳐 AX=XB에서 특정 에러를 줄이는 방식으로 진행 된다.
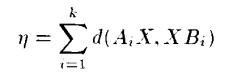
이때 d의 경우 유클리드 군에서 측정 된 거리이다. 리 그룹에 대한 정준좌표계를 사용하면 에러를 줄이는 문제는 간단하고 명시적인 해를 뽑아내는 least square fitting 문제로 재해석 될 수 있다.
Nadas 논문에서 아래 식을 최소화 하는 직교 행렬과 translation 의 명시적 표현을 보인다.
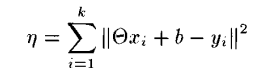
이때 최적의 직교 행렬과 b의 값은 오직 x와 y의곱의 합인 M 행렬에만 의존적이라는 걸 확인할 수 있었다. 이 사실과 정준 좌표계를 통해 AX=XB에 대한 최적의(best-fit) 결과를 얻을 수 있었다.
THE EUCLIDEAN GROUP
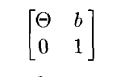
당연하게도, 위의 행렬을 강체의 운동에 대한 유클리드 군이며, SE(3)로 볼 수 있다. 이때 세타는 SO(3)에 포함되며, b는 유클리드 군에서의 3차원 벡터 값에 해당한다. 그냥 단순하게 T 행렬이라는 뜻.
리 군와 연관 된 모든 리 대수는 리 대수이다(?). 일반적으로 리 대수는 아래와 같은 조건들을 만족하는 이중 선형 맵과 함께 벡터 공간이다.
이때 선형 맵은 아래와 같고
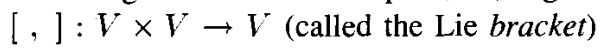
이는 아래를 만족한다. 이를 리 대수라고 부른다. (리 대수에 대한 자세한 내용은 리 군을 공부하자.)
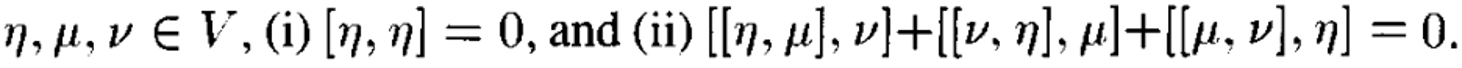
SO(3)의 리 대수는 는 so(3)로 표시되고 3 x 3 skew-symmetric 행렬의 형태이다. 이는 아래와 같이 표현한다.
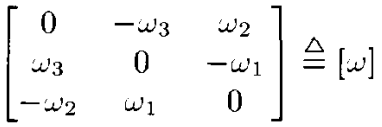
SE(3)의 리 대수는 se(3)로 표시되고 아래 형태의 4 X 4 행렬이며 se(3), so(3) 둘 다 Lie bracket은 행렬 교환자 (matrix commutator)에 의해 주어진다.
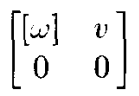
리 그룹의 근본적인 컨셉은 지수함수(exponential) 맵핑이다. 리 그룹 G가 있고, 이에 대응하는 행렬 리 대수 g가 있을 때 지수 함수 매핑은 아래와 같이 단순히 g를 G로 매핑하는 형태이다.
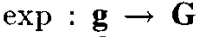
이때 매핑 함수는 아래와 같다. A행렬은 리 대수에 포함 되는 행렬.
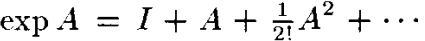
특정 리 대수에 포함 되는 집합 U가 있을 때, U -> G에 대한 매핑은 diffeomorphism 이다. diffeomorphism에 대한 자세한 내용은 https://elementary-physics.tistory.com/48 (솔직히 공부할 수록 뭔 개소리야 저절로 나온다. 추후에 리 그룹에 대한 공부는 여기를 참고해도 좋을 듯....) 따라서 지수함수는 로컬 좌표계를 리 그룹 G에 있는 identity처럼 정의 한다. (원본 : The exponential therefore defines local coordinates over some neighborhood of the identity in G) 이때의 좌표계를 정준좌표계(canonical coordinates)라고 한다.
논문에서는 정준좌표계에서 SE(3)와 SO(3)에 대한 명시적인 식을 유도하게 된다. 이때 근본적인 screw 이론에서의 결과가 사용되는데, 이는 모든 강체 모션은 rotation과 translation로 표현될 수 있다는 점이다. 이는 수학적으로 지수함수는 se(3)를 SE(3)로 매핑하는 데 사용된다(?)정도로 정의 될 수 있다. 즉, SE(3)에 포함되는 X가 있다면, se(3)에 포함되는 x가 존재하고 exp x = X 가 가능하다는 뜻이다.
so(3)에서 SO(3)에 대한 지수함수 매핑은 아래 식을 통해 이뤄진다.
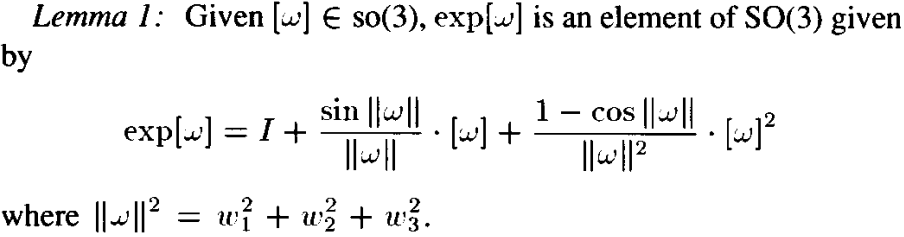
이 lemma로 SO(3)는
3차원의 공형태로 표현 될 수 있다.
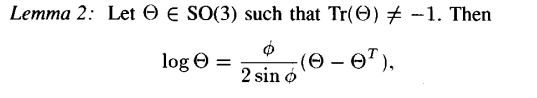
특정 theta가 SO(3)에 포함되고 theta의 Trace 값이 1이 아닐 때는 아래와 같은 식을 만족한다.
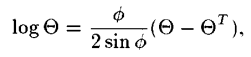
이때 파이는 아래 식 조건들을 만족한다.
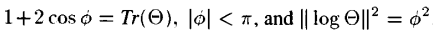
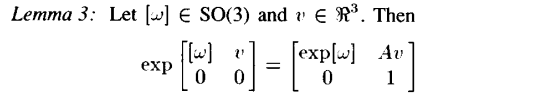
[w]가 SO(3)에 속하고 v가 실수 벡터라면 이들 행렬은 exp형태로 나타낼 수 있고 이는 SE(3)의 요소가 된다. 이때 A 행렬의 경우 Lemma1 을 참고하면 아래와 같이 나타내진다.
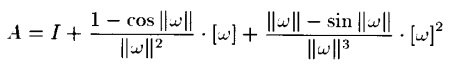
SO(3)의 경우처럼? exponential map은 모든 SE(3)에 대한 local 좌표계의 집합을 제공한다. 단, theta의 Trace가 -1인 경우만 제외하고. 이 집합에서 로그(logarithm)는 4번째 공식으로 주어진다.

기본적인 Lie 그룹/대수에 대한 내용은 여기까지다. 지금부터는 AX=XB에 대한 해를 찾는 작업을 해보자.
SOLUTION TO AX=XB
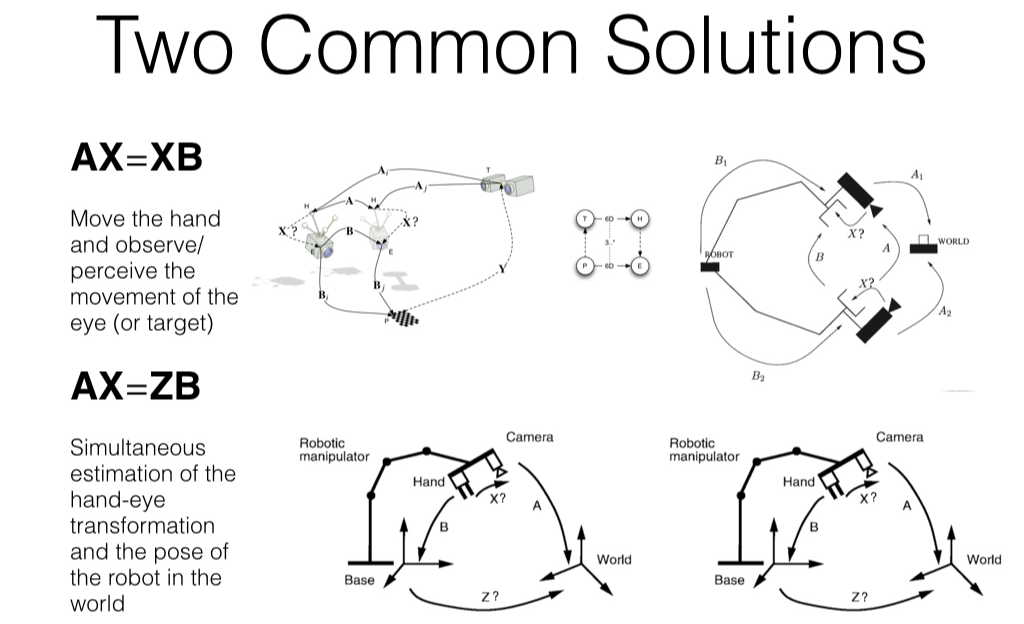
AX=XB에 대한 해는 위와 같은 경우에 사용된다. 주로 Hand eye calibration에 사용된다. AX=XB식을 행렬 식으로 구성하면 아래와 같다.
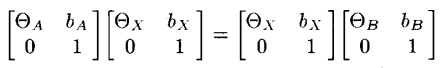
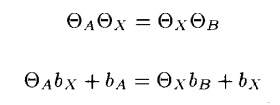
먼저 SO(3)에서 고려해보자. 즉 A,B,X모두 SO(3)의 요소라고 생각하자.
한가지 해가 있다는 조건으로 진행해보자. SO(3)에서 AX=XB의 해는 ||logA|| = ||logB||를 만족해야만 존재한다.이에 대한 증명은 생략한다. 논문을 참고하자.
정리1번
A와 B를 SO(3)의 요소라고 해보자. 이때 A와 B의 Trace는 -1이 아닌 경우라 하자. A와 B의 로그는 [alpha], [beta]로 표기하자. 이때 AX=XB의 particular solution이 Xp이며 이는 SO(3)에 속하는 경우 해는 아래와 같이 표현된다.
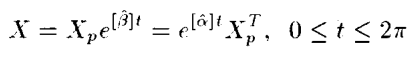
증명
AX=XB를 canonical coordinate 형태로 변환하면 아래와 같이 표현할 수 있다.
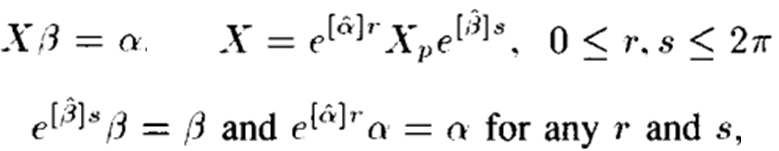
각 A와 B를 로그 형태로 만든 alpha와 beta의 경우 벡터 형태이기 때문에 자기 자신에 대한 회전 r, s에 의해 변하지 않기 때문에 위와 같은 식 형태로 나타낼 수 있다. 또한 Xp가 particular solution이므로 Xp*beta = alpha와 같은 표현이 가능하다. 따라서 X가 AX=XB식을 만족하게 된다.
일반적인 행렬 연산 특징으로 아래와 같은 식 변환을 진행할 수 있다.
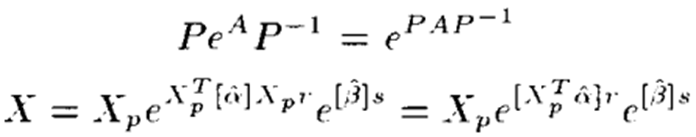
이때 Xp^T*alpha= beta이므로 아래와 같이 식을 수정할 수 있다. 이때 t = r+s.
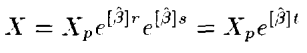
비슷한 식 형태로는 아래도 가능하다.
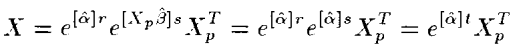
SO(3)에서 Unique Solution 찾기
SO(3)에서 AX=XB 식의 경우 한개의 파라미터 해만 가지고 있다. Unique solution을 찾기 위해서는 적어도 2개의 식은 있어야 하는데, 먼저 해가 존재한다고 가정하고 들어가보자. 간단하게 A,B를 2개의 쌍으로 만들어서 진행하면 된다.
정리2번
A1, B1 A2,B2가 SO(3)에 속하고 Trace가 -1이 아니라고 하자. 각각의 log norm값도 동일하다. 이때 각 세트에 대한 AX=XB의 해 X는 logA1 * log A2 !=0 , logB1 * log B2 !=0 인 경우에만 유일해가 된다.
증명
간단하게 logB1 * logB2 = 0 이라고 하면, B에 대한 벡터는 특정 스칼라 값을 곱해서 표현할 수 있게 된다. beta1= c*beta2. 이 뜻은 X*beta = alpha 식을 만족하는 X가 Unique하지 않다는 뜻이 된다.
SE(3)에서 Solution 찾기
앞서 언급했던 AX=XB 문제를 아래와 같은 식으로 표현할 수 있다.
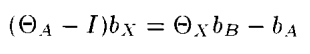
유일해(Unique Sol)을 찾기 위해서는 A,B가 2개가 있어야 하고, 이들은 특정 조건에서의 회전을 만족하여야 한다고 했다. 각 A값과 B값에 노이즈가 없고 물리적으로 해가 존재한다면 해는 무조건 존재한다. A,B 집합의 회전행렬이 정리 2번의 조건을 만족한다면 유일해 theta_x를 구할 수 있다. theta_x 값을 아래 식에 넣으면
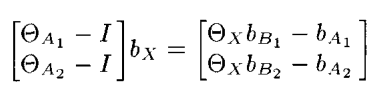
b_x에 대한 유일해도 구할 수 있다. 유일해를 증명하는 이야기도 있는데, 이건 이해가 잘 안된다.
Least squre Solution 찾기
실제 측정값에 대한 노이즈가 없을 수는 없기 때문에 best fit solution을 찾아야 한다. A,B에 대한 측정 된 값들을 통해 X를 구하려고 할 때 특정 에러를 최소화 하는 식을 사용한다.
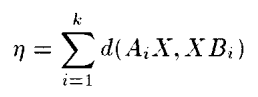
d의 경우 SE(3)에서의 적당한 거리 표현이 된다. d의 경우 아래 식으로 표현된다. 이때 || ||는 유클리디안 Norm.
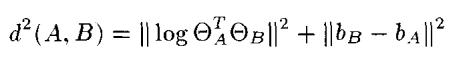
Lie group 방식의 장점은 canonical coordinate 형태가 문제를 linear least square fitting 형태로 정의할 수 있게 해준다는 것이다. 그러면 해는 간단한 형태를 띄게 된다. 앞서 말했던 식을 로그화 하여 매핑하게 되면 간단하게 바꿀 수 있다.

Nadas 논문에 보면 유클리디안 공간에서 x1~xp, y1~yp가 주어졌을 때 특정 에러값을 최소화하는 translation b와 orthogonal matrix theta은 아래식과 같이 명시적으로 표현 될 수 있다고 한다.
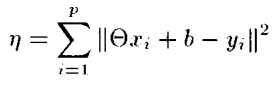
이 식에서 중요한 부분은 특정 매트릭스만이 에러값에 영향을 준다는 것이다.
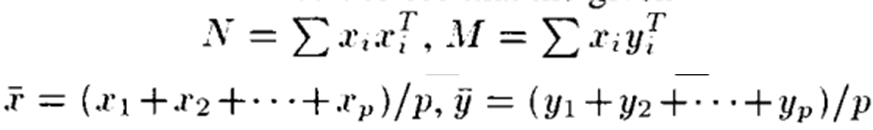
이를 이용해서 theta와 b를 간단하게 정리하면 아래와 같다.
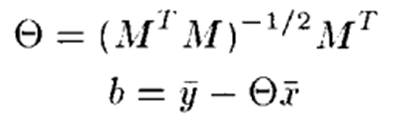
theta 값에 따라 b의 값은 유일값이 된다. 또한 theta 값도 M'*M 값이 싱귤러가 아니고 동일한 eigen value가 없을 경우 유일하게 된다. Calibration 문제에 적용하여 A,B 측정 값들이 있다고 가정하고 특정 에러를 최소화하는 식을 만들어보자.
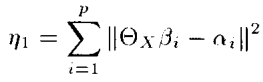
theta_x를 우선 찾고, b_x를 찾기 위한 식을 정리하면
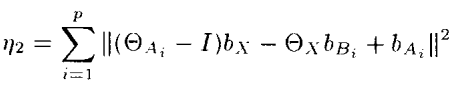
이때 최적의 theta_x는 아래 식을 통해 구할 수 있다.
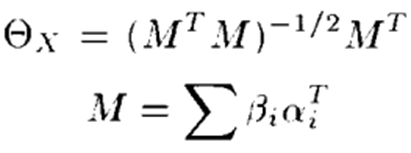
theta_x를 구하고 나서 bx를 구하는 식의 경우 일반적인 least -squre 해 형태로 아래 식 형태로 진행 된다.
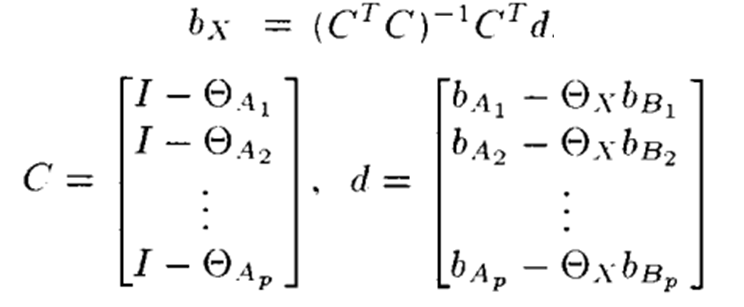
이를 통해 AX =XB에 대한 해를 구할 수 있게 된다.
EXAMPLE

from scipy.linalg import sqrtm
from numpy.linalg import inv
import numpy
from numpy import dot, eye, zeros, outer
from numpy.linalg import inv
A1 = numpy.array([[-0.989992, -0.14112, 0.000, 0],
[0.141120 , -0.989992, 0.000, 0],
[0.000000 , 0.00000, 1.000, 0],
[0 , 0, 0, 1]])
B1 = numpy.array([[-0.989992, -0.138307, 0.028036, -26.9559],
[0.138307 , -0.911449, 0.387470, -96.1332],
[-0.028036 , 0.387470, 0.921456, 19.4872],
[0 , 0, 0, 1]])
A2 = numpy.array([[0.07073, 0.000000, 0.997495, -400.000],
[0.000000, 1.000000, 0.000000, 0.000000],
[-0.997495, 0.000000, 0.070737, 400.000],
[0, 0, 0,1]])
B2 = numpy.array([[ 0.070737, 0.198172, 0.997612, -309.543],
[-0.198172, 0.963323, -0.180936, 59.0244],
[-0.977612, -0.180936, 0.107415, 291.177],
[0, 0, 0, 1]])
def logR(T):
R = T[0:3, 0:3]
theta = numpy.arccos((numpy.trace(R) - 1)/2)
logr = numpy.array([R[2,1] - R[1,2], R[0,2] - R[2,0], R[1,0] - R[0,1]]) * theta / (2*numpy.sin(theta))
return logr
def Calibrate(A, B):
n_data = len(A)
M = numpy.zeros((3,3))
C = numpy.zeros((3*n_data, 3))
d = numpy.zeros((3*n_data, 1))
A_ = numpy.array([])
for i in range(1):
alpha = logR(A[i])
beta = logR(B[i])
alpha2 = logR(A[i+1])
beta2 = logR(B[i+1])
alpha3 = numpy.cross(alpha, alpha2)
beta3 = numpy.cross(beta, beta2)
M1 = numpy.dot(beta.reshape(3,1),alpha.reshape(3,1).T)
M2 = numpy.dot(beta2.reshape(3,1),alpha2.reshape(3,1).T)
M3 = numpy.dot(beta3.reshape(3,1),alpha3.reshape(3,1).T)
M = M1+M2+M3
theta = numpy.dot(sqrtm(inv(numpy.dot(M.T, M))), M.T)
for i in range(n_data):
rot_a = A[i][0:3, 0:3]
rot_b = B[i][0:3, 0:3]
trans_a = A[i][0:3, 3]
trans_b = B[i][0:3, 3]
C[3*i:3*i+3, :] = numpy.eye(3) - rot_a
d[3*i:3*i+3, 0] = trans_a - numpy.dot(theta, trans_b)
b_x = numpy.dot(inv(numpy.dot(C.T, C)), numpy.dot(C.T, d))
return theta, b_x
X = numpy.eye(4)
A = [A1, A2]
B = [B1, B2]
theta, b_x = Calibrate(A, B)
X[0:3, 0:3] = theta
X[0:3, -1] = b_x.flatten()
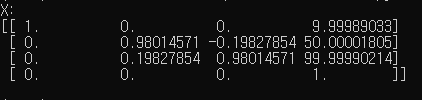
print("X: ")
print(X)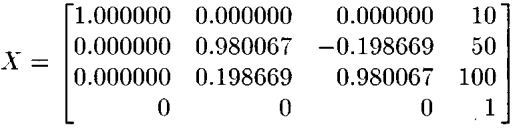
'미니멀공대생 > Control' 카테고리의 다른 글
| Mobile manipulator 101 :: Combined Jacobian & Dual trajectory (0) | 2022.10.03 |
|---|---|
| Mobile manipulator 101 :: Basic Kinematics (1) | 2022.10.01 |
| MIT 6.800/6.843 Robotics Manipulation :: Introduction (1) | 2022.06.21 |
| MIT 6.800/6.843 Robotics Manipulation :: Basic Pick and Place Part1 (1) | 2022.06.21 |
| MIT 6.800/6.843 Robotics Manipulation :: Motion planning(1) (1) | 2022.04.27 |
