티스토리 뷰
<The Problem With DDPG : Understanding Failures In Deterministic Environments With Sparse Rewards>
작성자 : 한양대학원 융합로봇시스템학과 유승환 석사과정 (CAI LAB)
정말 오랜만에!!! 작성하는 논문 리뷰입니다!ㅎㅎ 올해 저는 6축 협동로봇 UR5e에 강화학습을 적용하는 연구를 진행하고 있습니다! 첫 강화학습 연구다보니 감을 익혀보기 위해 action space의 차원을 간략화 시켜서, 앤드이펙터의 x, y 좌표, 즉 2차원의 action space를 가지고 DDPG 모델을 진행하고 있습니다ㅎㅎ 그런데... 학습을 진행할수록 x, y 좌표가 한 방향으로 증가 혹은 감소하는, 즉 한 point로 수렴해서 갇히는 문제가 발생하고 있습니다ㅜㅜ 그래서 DDPG의 한계점 및 해결책을 파악하고자, 이번 논문을 리뷰하고자 합니다! 그럼 시작하겠습니다~!! :)
1. 참고 링크 (원문) : https://arxiv.org/abs/1911.11679
The problem with DDPG: understanding failures in deterministic environments with sparse rewards
In environments with continuous state and action spaces, state-of-the-art actor-critic reinforcement learning algorithms can solve very complex problems, yet can also fail in environments that seem trivial, but the reason for such failures is still poorly
arxiv.org
2. DDPG 논문 리뷰 : https://ropiens.tistory.com/96?category=962955
강화학습 논문 정리 2편 : DDPG 논문 리뷰 (Deep Deterministic Policy Gradient)
작성자 : 한양대학원 융합로봇시스템학과 유승환 석사과정 (CAI LAB) 이번에는 Policy Gradient 기반 강화학습 알고리즘인 DDPG : Continuous Control With Deep Reinforcement Learning 논문 리뷰를 진행해보겠..
ropiens.tistory.com
0. Abstract
- 실제 환경은 Continuous한 state와 action space를 지니고 있고, SOTA actor-critic (reinforcement learning) 알고리즘들은 이러한 상황의 문제를 잘 해결할 수 있지만, 아직도 몇몇의 문제에 대해서는 실패하는 문제점이 있다.
- 실패하는 이유 중 하나는 실패의 원인에 대한 정확한 원인 분석이 미흡하기 때문이다.
- 본 연구에서는 reward가 sparse하고 deterministic한 환경의 특별한 경우에 이러한 실패에 대한 공식적인 설명을 정리한다.
- * reward가 sparse하다 : 시도한 action의 수에 비해 reward를 받는 횟수가 적다.
- * 환경이 deterministic하다 : 다음의 state가 현재의 state와 action으로 결정될 수 있는 환경


- 먼저, 매우 간단한 제어 문제를 사용하여, RL 학습 알고리즘(ex : DDPG)이 고정된 point(좌표)에 갇히는(수렴하는) 현상을 보여준다.
- 그 다음, 이러한 학습 알고리즘들이 수렴하는 현상에 대해 이해할 수 있는 기본 메커니즘에 대한 상세한 분석을 본문에서 제공한다.
- 이러한 분석을 통해, 위와 같은 학습 수렴 문제에 대해서 기존 해결책과 다른 새로운 해결책을 제시한다.
1. Introduction
<DDPG의 문제를 해결하기 위한 기존의 방법 및 한계점>
- DDPG는 deterministic policy를 이용하여 continuous한 state, action space를 제어할 수 있는 Deep Reinforcement Learning (RL) 알고리즘이다.
- 그러나 DDPG는 특정 좌표로 수렴하는 불안정성(Instability)을 지니는 단점이 있다.
- 다양한 RL 학습 알고리즘들은 이러한 불안정성 문제를 해결하기 위해, over-estimation bias와 같은 문제를 해결함으로써 안정성을 향상시켰다.
- ex) TD3 (Twin Delayed DDPG) : https://ropiens.tistory.com/89
TD3 리뷰 : Addressing Function Approximation Error in Actor-Critic Methods
editor, Junyeob Baek Robotics Software Engineer /RL, Motion Planning and Control, SLAM, Vision - 해당 글은 기존 markdown형식으로 적어오던 리뷰 글을 블로그형식으로 다듬고 재구성한 글입니다 - ori..
ropiens.tistory.com
- 하지만 불안정성 현상에 대한 근본적인 이해가 여전히 결여되어 있기 때문에, 위와 같은 임시방편적 해결책이 불안정성의 원인을 실제로 해결하는지에 대한 여부는 불확실하다.
- 따라서 매우 단순한 환경에서도 이러한 RL 학습 알고리즘이 실패할 수 있는 이유를 더 잘 이해하는 것이 중요하다.
- * 실패하다 : 학습에 실패하다, 특정 좌표로 수렴한다.
<DDPG가 실패하는 현상에 대한 분석>
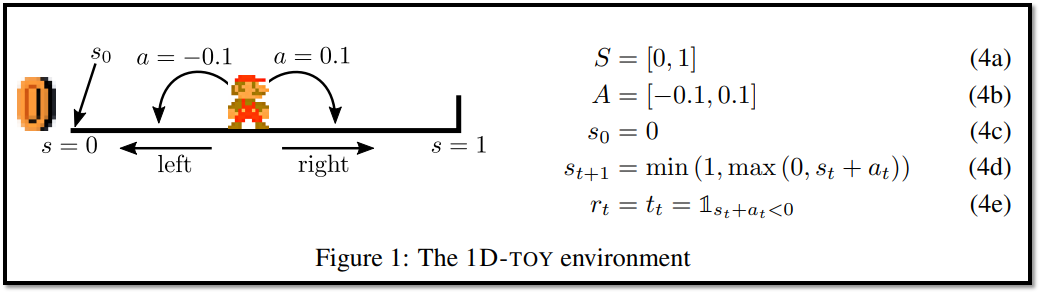
- DDPG가 실패하는 현상에 대해 조사하기 위해, 본문의 4절에서 sparse한 reward를 가지는 1차원 환경을 소개한다. (위 사진의 1D-toy Env)
- DDPG는 이 환경에서 종종 학습에 실패하는데, 이 현상을 분석하는 것이 중요하다.
- 그 다음, sparse한 reward와 deterministice case에서 작동하는 순환 메커니즘을 밝혀내서, poor policy로 빠르게 수렴하는 원인을 증명한다. (구체적인 설명은 4절에서 진행합니다!)
- 특히, 학습 초반에 reward를 받는 것이 충분하지 않을 때, 이러한 순환 메커니즘으로 인해 actor network도, critic network도 더 이상 발전할 수 없는 deadlock 상태를 초래할 수 있다는 것을 보여준다.
- 중요한 것은 agent가 reward를 받은 sample(RL 데이터 : state, action, reward, next_state)로 학습을 진행해도, 이 deadlock 상태가 지속된다는 것이다.
<새로운 해결책 제시>
- 이러한 메커니즘에 대한 연구는 function approximation의 효과가 무시되는 단순화된 맥락에서 공식 증명으로 뒷받침된다.
- 그럼에도 불구하고, 이러한 결과를 이해하는 것은 Neural Network로 구현된 actor와 critic을 사용할 때 직면하는 실제적인 현상을 분석하는 데 도움이 된다.
- (위 밑줄 친 부분은 아직 이해가 안됩니다... 좀 더 공부해보고 다듬어보겠습니다!)
- 이러한 새로운 관점에서, 본문에서는 RL 학습 알고리즘의 올바르지 않는 수렴 과정에 대응할 수 있는 몇 가지 기존 알고리즘을 5절에서 재검토하고, 이러한 문제에 대한 대안적인 해결책을 제안한다.
2. Related Work와 3. Background는 추후 작성하겠습니다.
4. A New Failure Mode
<4절 개요>
- 4절에서는 간단한 environment를 소개하는데, 우리는 이 환경을 1D-toy라고 부른다.
- 이것에 대한 설명은 아래의 그림과 같다.
- ======================================================
- time : discrete
- state : 0~1 (continuous)
- action : -0.1~0.1 (continuous)
- initial state : 0
- next_state :
- -> s_t + a_t가 0보다 작으면, next_state = 0
- -> s_t + a_t가 0보다 크고 1보다 작으면, next_state = s_t + a_t
- -> s_t + a_t가 1보다 크면, next_state = 1
- reward : s_t + a_t가 0보다 작으면 1 (왼쪽으로 가면 보상 받음)
- ======================================================

- 1D-toy 환경은 state와 action이 1차원적인 단순한 환경임에도 불구하고, DDPG는 이 환경에서 실패할 수도 있다.
- 먼저, DDPG가 100% 성공을 달성하지 못한다는 실험 결과를 보여준다.
- 만약 policy를 학습하는 것을 초반에 성공하지 못한다면, learning process가 stuck될 수 있다는 결과를 보여준다.
- * stuck되다 : 한 좌표로 수렴한다. (ex : 계속 오른쪽 방향으로 0.1만큼 이동)
- 또한 초기 actor network가 첫 reward를 찾기 전에, 초기 단계에서 상당히 수정될 수 있다는 것을 보여준다.
- * reward를 찾다 : 양의 reward를 얻다
- 이러한 현상을 종합하여 어떻게 deadlock 상황을 초래하는지 설명한다.
- 이러한 경우에 발생하는 바람직하지 않은(undesirable) 순환 과정을 밝히고 공식적으로 연구함으로써 이 설명을 deterministic하고 sparse한 reward 환경에 일반화한다.
- 마지막으로, 우리는 이 순환 과정에 들어가는 것의 결과를 탐구한다.
4.1 Empirical Study
- 모든 실험에서 최대 에피소드 길이(N)을 50으로 설정했지만, 관촬되는 state는 다른 값들과 함께 지속된다. (매 에피소드마다 state가 다르다는 것을 의미하는 것 같습니다~!)
4.1.1 Residual Failure to converge using different noise process : Probabilistic VS OU
- 1D-TOY 환경에서 DDPG 알고리즘을 학습시켰다.
- 이 환경에서는 왼쪽으로 조금만 걸어도 보상을 받고, 에피소드가 끝나도 보상을 받을 수 있는 쉬운 환경이기 때문에 DDPG가 100% 성공할 것이라고 예상한다.
- 그러나 Figure 2a를 보면, Ornstein-Ulenbeck(OU) noise process를 사용한 첫 번째 시도는 DDPG가 성공한 경우가 94%에 불과하다는 것을 보여준다.
- * OU noise process란? : 추후 정리하겠습니다!
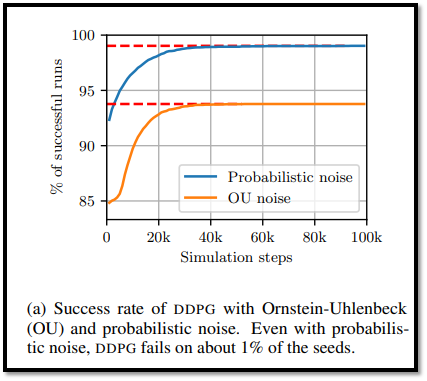
- 이러한 실패는 exploration 문제에서 비롯될 수 있다.
- 실제로 각 에피소드가 시작될 때, OU noise는 0으로 재설정되고 에피소드의 첫 단계에서 OU noise는 거의 발생하지 않는다.
- 즉, 초기에는 exploration을 거의 할 수 없다.
- 이러한 단점을 제거하기 위해, OU noise process를 "probabilistic noise"이라고 부르는 ε-greedy와 유사한 exploration 전략으로 대체한다.


- 본문에서는 ε = 0.1로 설정하여, 10% 확률로는 random한 action을, 90% 확률로는 actor network의 action을 취했다.
- 이를 통해 모든 policy에 대해 각 에피소드의 첫 번째 단계에서 최소 5%의 성공 확률을 보장할 수 있다.
- 그러나 Figure2-(a)를 보면, probabilistic noise를 사용함에도 불구하고, DDPG의 성공률은 99%에 그쳤다.
- 참고로, 이후의 실험은 모두 probabilistic noise를 사용하였다.
<Exploration의 충분 및 불충분에 따른 결론>
- 이러한 실패를 분석했을 때, actor network의 출력이 항상 오른쪽으로 가는 saturated policy로 수렴했음을 관찰한다. (모든 state s에서 π(s)=0.1)
- * saturated policy : 모든 상태에 대해 같은 action을 출력하는 policy (stuck된 현상)
- 그러나 probabilistic noise 때문에 agent가 왼쪽으로 이동하는 경우가 있기 때문에, 일부 mini-batch sample(state, action, next_state, reward)은 reward가 0이 아니다.
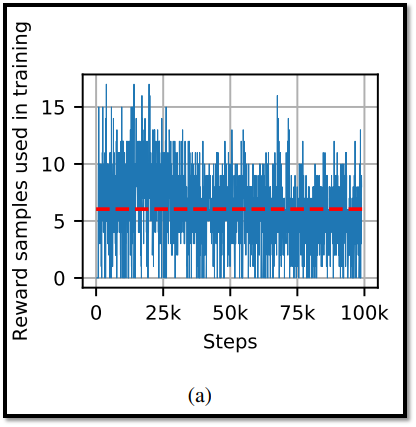
- Figure 3-(a)는 1D-toy 환경에서 DDPG를 학습 할 때, replay buffer에서 가져온 mini-batch의 reward 발생을 보여주며, 100개의 mini-batch 중 reward를 받는 batch는 평균 6.03개 밖에 안된다.
- 학습 중에 mini-batch에서 보상받는 batch(sample, trainsition이라고도 부릅니다!)가 꾸준히 존재한다는 것은 이 환경에서 DDPG의 실패가 behavior policy에 의한 불충분한 exploration으로 인한 것이 아님을 의미한다.
4.1.2 Correlation between finding the rewards early and finding the optimal policy
- 위 실험 결과에서 DDPG가 정기적으로 reward를 찾음에도 불구하고, 1D-toy env에서 stuck될 수 있음을 보았다.
- 이번 실험 결과에서는 DDPG가 학습 초반에 reward를 찾을 때, 최적의 policy로 수렴하는 데 더 성공적이라는 것을 보여준다.
- 반면에 첫 reward가 늦게 발견되면, 학습 과정은 종종 sub-optimal policy에 stuck된다.
- Figure 3-(b)에서, 초기 단계는 학습의 성공 여부에 큰 영향을 미치는 것으로 보인다.
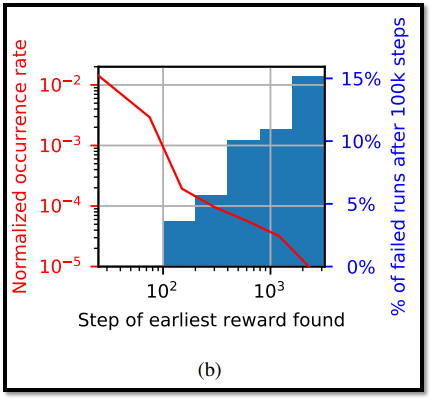
- Figure 3-(b)에서 첫 reward가 50 steps 이내에 발견되면, DDPG의 성공률은 100%이다.
- 그러나, 첫 reward가 50 steps 이후에 발견되면, DDPG의 성공률은 96%로 떨어지고, reward가 더 늦게 발견되면 87%까지 떨어진다.
- 따라서, 학습 초기 단계에서 reward를 빠르게 찾는 것은 중요하다.
4.1.3 Spontaneous actor drift
- 각 학습 초기 단계에서 DDPG의 actor와 critic network의 출력 값(state-action values, action values)이 0에 가깝게 출력되도록, 네트워크 파라미터 값이 초기화된다.
- 게다가 agent가 reward를 오랫동안 찾지 못할수록 gradient 값이 미미해지므로, 첫 reward가 발견되기 전 까지 actor와 critic의 출력 값은 일정한 값을 유지될 수도 있다.
- 실제로 reward를 찾지 못했을 때, actor network가 빠르게 saturated 상태에 도달하는 것을 보여준다. (아래의 Figure 4-(b) 참조)
- 이를 증명하기 위해, 보상이 없을 때의 1D-toy의 결과 : Figure 4를 보아라.

- Figure 4를 봤을 때, critic 출력 값(a)은 초반에 진동하다가 점차 수렴하는 것을 볼 수 있지만, actor 출력 값(b)는 빠르게 0.1 혹은 -0.1로 수렴하는 것을 볼 수 있다.
- Figure 4-(b)는 reward가 없을 때, actor network는 saturate policy로 빠르게 수렴할 수 있다는 것을 보여준다.
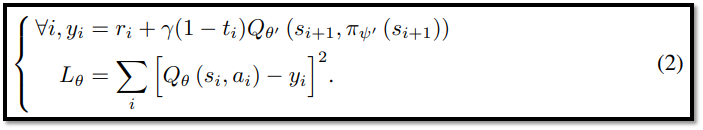
- Figure 4-(a)에서 critic의 loss function이 수식 (2 : MSE)이기 때문에, reward가 없을 때 max|Q| 값이 증가할 수 있다는 사실은 직관에 어긋나는 것처럼 보일 수 있다.
- 그러나 하나의 input (state, action)에 대한 Q 값이 증가하면, 다른 input에 대해서도 Q 값이 증가할 수 있으므로, Q의 global maximum이 증가할 수 있다는 점에 유의해야 한다.
- 이 현상이 critic이 학습 할 때 발생하는 over-estimation 현상의 핵심이지만, 본문에서는 이에 중점을 두지는 않는다.
4.2 Explaining The Deadlock Situation For DDPG on 1D-TOY
<4.2절 개요>
- 4.1절에서는1D-TOY 환경이 단순함에도 불구하고, DDPG의 실패율이 1% 정도인 것을 보여주었다.
- 4.2절에서는 1D-TOY 환경에서 DDPG가 Deadlock이 발생하는 메커니즘을 설명하는 데 필요한 요소를 설명할 것이다.
<Deadlock이 발생하는 원인 분석>
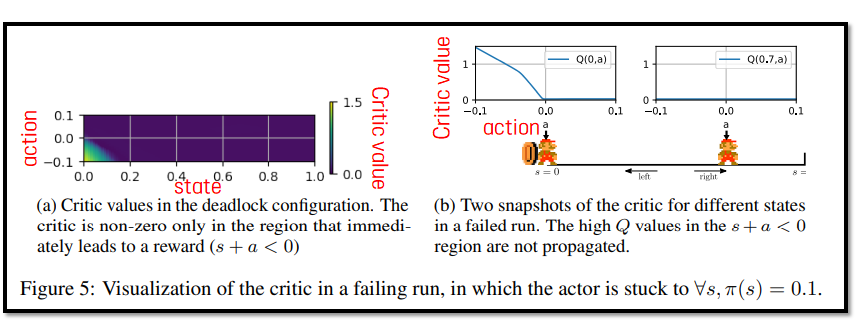
- Figure 5는 1D-TOY 환경에서 DDPG가 실패할 때의 critic 값이다.
- Figure 5-(a)를 보면, reward의 값이 reward가 발견되는 지역(s+a < 0) 밖으로 올바르게 전파되지 않음을 볼 수 있다. (state > 0.1 이상에서는 critic value가 모두 0인 것을 볼 수 있음)
- Deadlock의 핵심은 actor가 오른쪽 행동(π(s)=0.1)으로 전환되면, actor network의 파라미터는 equation (3)의 빨간 박스 값에 따라 업데이트된다는 것이다.
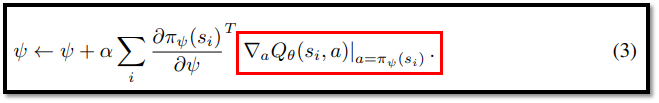
- Figure 5-(b)는 action = 0.1 일 때 critic(Q) 기울기는 0이므로(파란색 직선) actor는 업데이트 되지 않는다.
- 게다가 critic network는 target : y = r(s, a) + γQ(s', π(s'))과 차이가 없도록 업데이트 되는데(Mean Squared Error), Q(s', π(s')) = Q(s', 0.1)이 0이기 때문에, target : y = r(s, a)가 된다.
- 즉 critic의 target은 오로지 reward를 받은 action에 대해서만 non-zero가 되며, reward를 받지 않은 action은 모두 0이 된다.
- sparse reward를 지니는 환경이기 때문에, 대부분의 action에서 critic은 업데이트가 되지 않는다.
- Q(s', 0.1) = 0이 된다는 사실이 deadlock을 유발시킨다.
<Deadlock과 optimal policy와의 상관 관계>
- Deadlock은 update를 하는데 사용되는 batch에 의존하지 않기 때문에(Q(s', 0.1) = 0에 의해 발생하기 때문에), Deadlock 상태에서 optimal policy를 적용해도 Deadlock을 해결할 수 없다.
- 본문에서는 20,000 step만큼 학습 후, optimal policy로 behavior policy를 대체하여 이 실험을 수행했다.
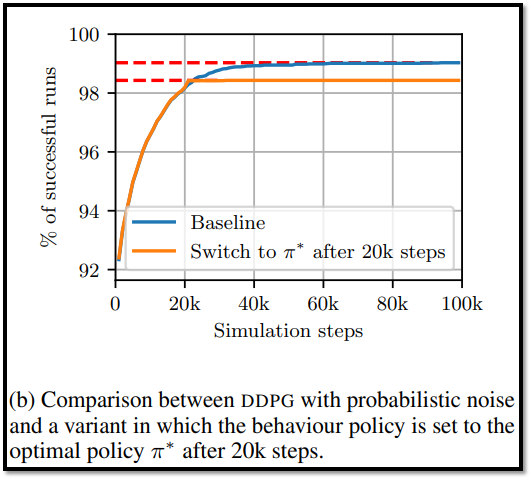
- 결과는 Figure 2-(b)에 나와있으며, 이상적인 sample 및 policy가 제공되더라도, DDPG는 한번 stuck 되면 Deadlock에 갇히는 현상을 볼 수 있다. (주황색 선의 21~22k쯤을 참고)
- Baseline의 결과와 비교했을 때, reward를 초기에 찾는 것이 더 나은 성과로 이어지는 이유를 뒷받침 할 수 있다.
- reward를 초반에 충분히 찾으면, π(s_0)는 너무 많이 변하지 않고, a=π(s_0) 일 때의 Q(s_0, a)의 기울기는 올바른 방향으로 actor에 피드백을 줄 수 있다.
- 번외 : 그러나 actor가 오른쪽으로 이동하더라도, DDPG가 항상 실패하는 것은 아니다.
- 실제로, Deep Neural Network의 근사치 때문에 처음으로 reward를 찾을 때 critic의 형태는 다양하며, 때로는 critic이 수렴되기 전에 actor가 업데이트 될 수 있을 만큼 충분히 천천히 수렴된다.
<Deadlock Process 정리>

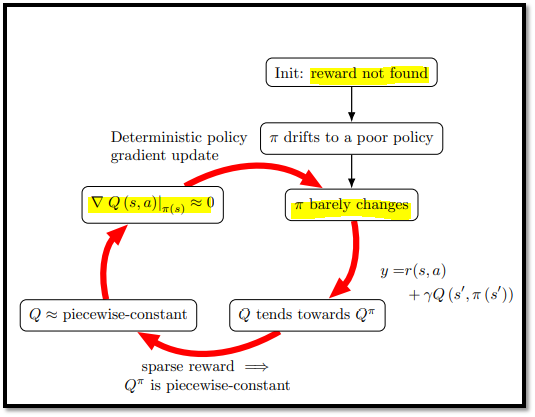
- 위 Figure 6은 Deadlock process를 요약한다.
- 왼쪽의 초록색 점이 start point이다.
- 먼저 actor는 모든 state에 대해 0.1(오른쪽 최대 값)으로 drift된다.
- 그 다음 critic은 기울기가 0이기 때문에 보상을 받을 때는 1, 아니면 0으로 수렴한다.
- 따라서 actor는 업데이트 되지 않는다. (=stuck, saturated policy)
4.3 Generalization
<4.3절 개요>
- 4.2절에서 본문의 1D-TOY 연구는 어떻게 DDPG가 이러한 단순한 환경에서 stuck될 수 있는지에 대해 밝혀냈다.
- 4.3절에서는 DDPG, TD3를 포함한 일반적인 continuous action을 학습하는 actor-critic 알고리즘의 넓은 맥락에서 일반화하여, deterministic하고 sparse reward를 지니는 환경에 적용한다.
- 일반회된 deadlock 매커니즘은 아래의 Figure 7에 설명되어 있다.
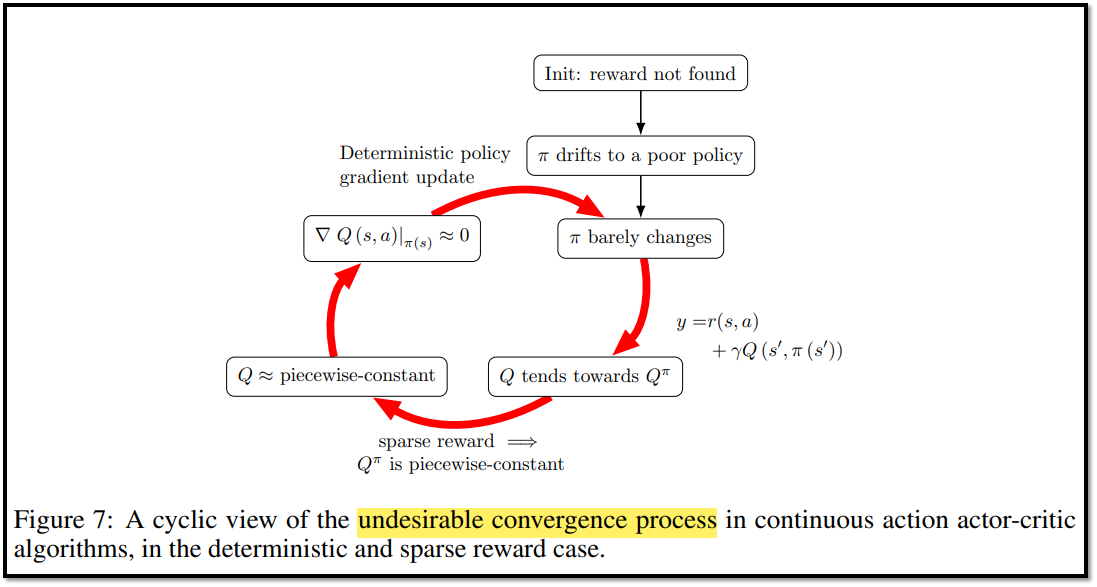
<Entry Point>
- behavior policy가 어떤 reward를 찾기 전에, actor와 critic을 훈련시키는 것은 여전히 actor가 나쁜 state에 빨리 도달하게 만드는 업데이트를 촉박시킬 수 있다.
- 이것을 Deadlock Process의 진입점(Entry Point)라고 정의한다.
<Q tends toward Qπ>
- critic이 policy(actor)보다 빠르게 업데이트 되면, critic의 업데이트 규칙(equation 2)에 의해 Q value는 Qπ로 수렴한다.
- 즉 보상을 받으면 1, 받지 않으면 0으로 수렴한다.
<Qπ is piecewise-constant>
- Qπ는 piecewise-constant인데, 그 이유는 Vπ(s')가 오직 2가지에 의존하기 때문이다.
- * piecewise-constant(계단 함수)란? : https://ko.wikipedia.org/wiki/%EA%B3%84%EB%8B%A8_%ED%95%A8%EC%88%98
계단 함수 - 위키백과, 우리 모두의 백과사전
수학에서, 계단 함수(階段函數, 영어: step function) 또는 조각마다 상수 함수(-常數函數, 영어: piecewise-constant function)는 정의역을 적절한 유한 개의 구간으로 분할하였을 때 각 구간에서 상수 함수
ko.wikipedia.org
- (1) : s'에서 rewarded state에 도달하는 데 필요한 step 수
- (2) : rewarded sate의 value
- 1D-toy에서는 actor의 값이 모든 state에 대해 0.1일 때, 이러한 현상이 발생한다.
- 쉽게 정리하자면, Qπ가 보상을 받으면 1, 받지 않으면 0으로 수렴하여서 계단 함수가 만들어진다는 의미이다.
<Q is approximately piecewise-constant and ∇aQ(s, a)|a=π(s) ≈ 0>
- Qπ는 계단 함수이고, Q는 Qπ를 향하도록 업데이트 되기 때문에, Q는 점차 계단 함수가 된다는 것을 유추할 수 있다.
- 이 사실의 영향은 4.5절에서 추가 설명을 할 것이다.
- Q는 계단 함수와 일치하도록 훈련되었기 때문에 대부분 평탄한 gradient를 가질 것이라고 예상할 수 있다.
- 즉, ∇aQ(s, a)|a=π(s) ≈ 0 이다.
- 그리고 결정적으로, 평탄한 gradient는 더 높은 값의 Q value에 도달하는 방법에 대한 정보를 거의 제공하지 않는다.
<π barely changes>
- DDPG는 equation (3)과 같이 deterministic policy gradient 업데이트를 사용한다.
- Q는 항상 (s, π(s))에서 미분하기 때문에, 이것은 확률성을 포함하지 않는 analytical gradient이다.
- 따라서 actor update는 behavior policy에 의해 reward가 정기적으로 발견되는 경우에도 중단된다.
4.4 Consequences of the Convergence Cycle
<Figure 7의 순환 결과>
- Figure 7의 빨간색 화살표에서 볼 수 있듯이, 수렴 과정에서 더 많은 루프가 수행될수록, critic의 값은 일정해지고, actor의 값은 stuck되는 경향이 발생한다.
- 중요한 것은 이 cycle 수렴 프로세스가 policy의 업데이트를 급격히 느려지거나 중지되게 만든다.
- 이러한 루프가 계속 발생한다면 최종 성과는 좋지 않아질 것이다.
<제목 입력>
- 추후 작성 예정
4.5 Impact of Function Approximation
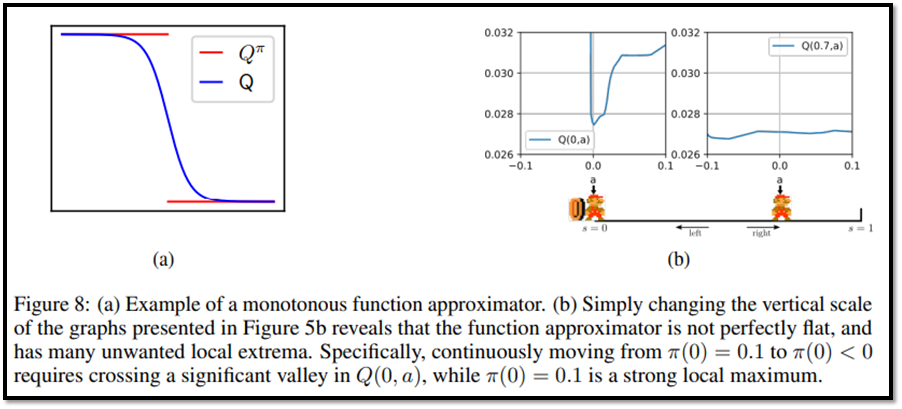
- 추후 작성 예정
5. Pontential Solutions
- 4절에서 DDPG와 TD3와 같은 actor-critic 알고리즘은 Figure 7에서 의존성이 강조된 세 가지 요소의 조합으로 인해 초기 수렴이 poor policy로 이어진다는 것을 보여줬다.
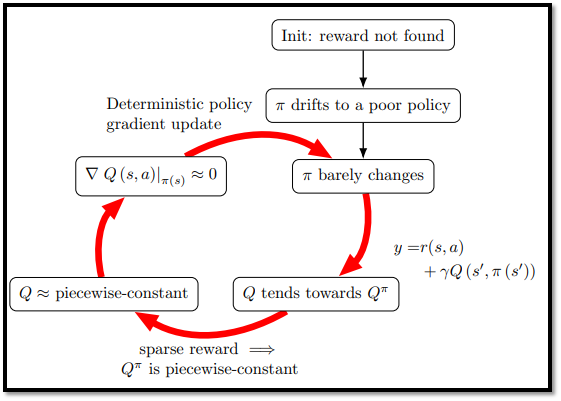
- 요소 (1) : deterministic policy gradient update의 사용
- 요소 (2) : critic update에서 Q(s', π(s'))의 사용
- 요소 (3) : deterministic 환경에서 sparse reward를 해결하려고 시도하는 것
- 5절에서는 위 요소로 인해 발생하는 이슈들을 해결하기 위해, 존재하는 혹은 잠재적인 솔루션들을 분류한다.
<Avoiding Sparse Rewards>
- 보상을 받는 횟수를 sparse에서 dense하게 변환하면, critic network가 더 이상 일정한 함수로 수렴되지 않기 때문에 위의 문제를 해결할 수 있다.
- 이러한 솔루션들은 주로 문제 의존적이며 보상 변환으로 bias를 유발할 수 있기 때문에, 본문에서는 더 이상 조사하지 않는다.
- 예시 (1) : Using Various Forms of Shaping
- * 논문 제목 : Autonomous Shaping: Knowledge Transfer in Reinforcement Learning (2006)
- * 논문 내용 : state의 기댓값을 action에 대한 기댓값으로 변경해서 학습에 사용한다는 내용
- 예시 (2) : Adding Auxiliary tasks
- * 논문 제목 : Reinforcement learning with unsupervised auxiliary tasks.
- * 논문 내용 : 보조적인 reward(task)를 추가한다는 내용
<Replacing the policy-based critic update>
- Replay Buffer에서 reward로 이어지는 transitions(state, action, next_state)이 발견되면, 이 transitions에 해당하는 critic update는 Q(s', π(s'))를 사용한다.
- 따라서 behavior policy가 찾은 next state의 value를 전파(propagating)하지 않는다.
- 몰론 critic에서의 미분 값을 사용할 때도, actor는 더 나은 policy를 반영하도록 π를 업데이트하는 경향이 있어야 하지만, critic이 항상 적절한 미분 값을 제공하는 것은 아니다. (Figure 7 참조)
- 만약 continuous action space에서 maximum 값을 취할 경우, 기존의 Q(s', π(s')) 대신에 max Q(s', a)를 사용하는 것은 이 문제를 해결할 수 있을 것이다.
- 우리는 이를 DDPG-argmax라고 부르며, 자세한 것은 부록 F.1에서 설명한다.
- DDPG-argmax는 1D-toy 환경에서 100% 성공률을 보여준다.
- 그러나 large action space를 가질 경우, 최적화가 어렵기 때문에 이러한 방법은 적절하지 않다.
- 이를 해결하기 위해 SAC (Soft Actor Critic)을 사용할 수도 있으며, 아래에서 추가적인 설명을 진행하겠다.
<Replacing the deterministic policy gradient update>
- deterministic policy gradient update에 의존하는 대신, 확률적(stochastic) policy에 의존하여 actor update를 수행할 수도 있으며, 이 경우가 SAC이다.
- SAC는 Q(s', π(s'))를 사용하지 않기 때문에, 여기에서 언급한 undesirable convergence process로 부터 해방될 수 있다.
- 또 다른 해결책은 CACLA를 사용하는 것인데, actor의 update에 regression 기법을 사용하는 것이다.
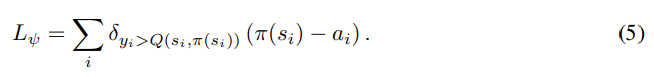
6. Conclusion And Future Work
- 강화학습에서 sparse한 reward를 지니는 환경에서 continuous action을 제어하는 것은 여전히 challenging 문제이다.
- 이러한 환경에서는 exploration이 reward를 찾기에 불충분할 때, 좋은 policy를 학습할 수 없다는 사실은 이미 널리 알려진 사실이다.
- 본문에서는 exploration이 충분하여도 actor-critic 알고리즘들이 stuck될 수 있으며, 이때 reward를 받은 transitions들은 무시된다는 것을 보여준다.
- 또한 위 문제들을 해결할 수 있는 기존에 존재하거나 잠재적인 솔루션들을 제공한다.
- 그러나, 본 실험은 간단한 벤치마크 : 1D-toy 환경에서만 검증이 되었다.
- 추후 연구로 더 복잡한 환경에서의 검증이 필요하다.
