티스토리 뷰
강화학습 논문 정리 3편 : DDQN 논문 리뷰 (Deep Reinforcement Learning with Double Q-learning)
hanyangrobot 2021. 6. 20. 15:19작성자 1 : 한양대학원 융합로봇시스템학과 유승환 석사과정 (CAI LAB)
작성자 2 : 한양대학교 로봇공학과 홍윤기 학부연구생
정말 오랜만에 팀블로그에 글을 작성해보네요ㅎㅎ 오늘은 value iter 기반 강화학습 알고리즘인 DDQN : Deep Reinforcement Learning with Double Q-learning 논문 리뷰를 진행하겠습니다!! 참고로 DDQN은 AAAI 2016에 출판(?)된 논문입니다~
링크 0 (원문) : https://arxiv.org/pdf/1509.06461.pdf
링크 1 (참고 블로그) : https://taek-l.tistory.com/36
[강화학습 Key Paper] Double DQN
본 포스트는 OpenAI에서 공개한 강화학습 교육자료인 Spinning Up의 도움을 받아, 강화학습(Reinforcement Learning, RL)에 대한 기초개념을 정리해보고자 제작한 시리즈의 일환입니다. 1)기초 지식 2)주요 논
taek-l.tistory.com
0. ABSTRACT
<Q-Learning의 단점>
- DQN(Deep Q-Network) 같이 이전의 Q-Learning 알고리즘들은 특정 조건에서 action value가 지나치게 커지는 overestimate 문제 발생
- overestimation 문제 = overestimate action value가 Network에서 Propagation
- 이러한 문제점에 대해 아래와 같은 질문을 할 수 있음
- (1) overestimate가 일반적(common)으로 일어나는 현상인가?
- (2) overestimate가 Q-Learning 알고리즘의 성능을 해치는가?
- (3) overestimate를 예방(prevent)할 수 있는가?
<본문에서 제시하는 내용 : 위 질문들에 대한 답안 제시>
- (1)에 대한 답 : DQN 알고리즘의 true action value와 estimate action value를 Atari 2600의 일부 게임에서 비교함으로써 상당한 overestimation이 발생하는 것을 확인
- * (5절 실험 결과 부분에서 확인 가능)
- * DQN (Deep Q Network) : Deep Neural Network와 결합된 Q-Learning
- * DQN 참고 링크 : https://ropiens.tistory.com/75?category=962955
강화학습 논문 정리 1편 : DQN 논문 리뷰 (Playing Atari with Deep Reinforcement Learning)
작성자 : 한양대학원 융합로봇시스템학과 유승환 오늘은 강화학습 논문 DQN : Deep Q-Networks를 리뷰해보겠습니다~! 강화학습의 기초를 공부할 때는 DQN, DDPG 논문을 공부하면 좋다는 github.com/CUN-bjy
ropiens.tistory.com
- (3)에 대한 답 : 본 연구에서 DQN에 Dobule Q-Learning을 적용함으로써 overestimation 현상을 줄일 뿐만 아니라, 다양한 게임에서 더 나은 성능으로 이어진다는 것을 보여줌
- * (5절 실험 결과 부분에서 확인 가능)
- * Double Q-Learing에 대해선 아래에서 설명할 예정
1. Intro
<강화학습의 목표 및 단점>
- 강화학습 목표 : Optimal policy(정책)을 학습하는 것 -> 누적된 미래의 reward(보상) 신호를 최적화 -->> Q-Value (action value) 최적값 찾기
- 강화학습 알고리즘 중 Q-Learning이 가장 유명함
- * policy : State s에서 Action a를 취할 확률을 모든 state 및 action에 대해 명시한 것
π(a|s)=P(a|s),∀s,∀a
- * Q-Learning : 보상에 대한 기댓값인 Q-Value를 학습하는 알고리즘

- Q-Learning의 'estimate of optimial future value'에 의해 Q-value가 지나치게 과대화(overestimate)되는 경향 존재
- Q-Learning 단점 : 이러한 overestimate로 인해 optimal 하지 않은 action value(Q-Value)를 학습하는 경우 존재
<overestimate는 실제 성능에 부정적인 영향을 미칠까?>
- 모든 Q-value가 높을 경우(=overestimate) action을 선택할 확률이 비슷해지므로, policy 학습에 악영향을 안줄 수도 있음
- 그러나 특정 action에 대해서 overestimate가 발생하는 경우, policy 학습에 악영향을 끼칠 수 있음
- * ex) 가위 바위 보 게임
- 실제 경우에서 overestimate가 발생하는지, 그리고 이것이 악영향을 끼치는지를 확인하기 위해 본 연구에서 최근 DQN 알고리즘의 성능 조사를 진행
- 이에 대한 내용은 아래에서 추가 설명
<새로운 해결책 : Double Q Learning Algorithm>
- 본 연구에서 DQN에 Double Q Learning 알고리즘을 적용하여 Double DQN이라는 새로운 알고리즘을 제안
- DDQN은 더 정확한 Q-Value 값을 산출할 뿐만 아니라 여러 게임에서 훨씬 높은 점수로 이어지는 것을 보여줌
- 이것은 DQN에 대한 overestimation이 실제로 더 나쁜 policy로 이어졌고, 이를 줄이는 것이 유익하다는 것을 보여줌
- 또한 DQN을 개선함으로써 우리는 Atari 도메인에서 최첨단 결과를 얻음
2. Background
<Q-Learing>
- 강화학습 문제 유형 : 순차적 의사결정 문제 (Sequential Decision Problems)
- 강화학습에서 학습하고자 하는 것 : optimal policy
- optimial policy를 어떻게 찾을까? : Q-Learning을 통해 얻어진 optimal Q-value를 통해 optimal policy를 구함
- Q∗(s, a) = maxπ Qπ(s, a).

- Q-Learning은 모든 state에 대한 Q-value를 학습하기 때문에 연산량이 많다는 단점 존재
- 이를 해결하기 위해 Q-value function을 파라미터화해서, 그 파라미터를 학습함
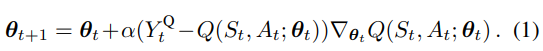
- 이때의 정답 값 : target Y는 아래와 같이 정의됨

<DQN : Deep Q Networks>
- DQN : Q-Learning에 Deep Neural Network를 결합
- Network's input & output : State s & Action values Q(s, ˙;θ) // θ: Network의 파라미터
- DQN에서는 아래의 2가지가 중요한 아이디어이며, 이들이 DQN 알고리즘의 성능을 향상시킴
- (1) target network 사용 : DQN의 네트워크와 동일한 구조이지만 다른 파라미터 θ-로 구성되며, 매 step τ 후에 origin network의 파라미터가 target network로 복사됨
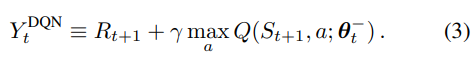
- (2) experience replay buffer 사용 : 관찰된 transition(state, action, next_state, reward)가 replay buffer에 저장되며, batch_size 값보다 커지면 이 buffer에서 random하게 sample하여 학습 진행 -> 시간에 따른 sample 간의 상관관계 제거
<Dobule Q-Learning>
- 위의 식 2, 3(Q-Learning & DQN)의 max 연산자에서 action을 선택하고 평가하는데 같은 파라미터를 사용
- * action을 평가한다 = Q-Network 업데이트를 위해 action value를 가져오기
- 이는 target Y를 optimal value보다 크게 추정함으로써 overestimate 현상이 발생하게 됨
- 이를 방지하기 위해 action의 선택과 평가를 분리함 (서로 다른 파라미터 사용) -> Dobule Q-Learning의 아이디어

- 기존의 Q-Learning, DQN의 target Y : 위와 같이 action의 선택과 평가할 때, 동일한 파라미터 θt를 사용 -> action을 평가할 때도 greedy policy가 적용되기 때문에 overestimate 현상 발생

- Dobule Q-Learning의 target Y : action을 선택할 때는 orgin network(내부 Q) 파라미터 θt를 사용 & action을 평가할 때는 target network(외부 Q) 파라미터 θ't 를 사용함 -> action을 평가할 때는 greddy policy 미적용 (target network는 environment과 상호작용을 안하기 때문)

3. Overoptimism due to estimation errors
<Q-Learing's overestimations 발생 원인>
- (원인 1) Using Function Approximation
- 참고 논문 : Issues in Using Function Approximation for Reinforcement Learning (Thrun and Schwartz, 1993)
- 내용 : action value가 [-ε, ε] 간격으로 균일하게 분포된 random error를 포함하는 경우, 각 target은 아래의 값까지 overestimate 될 수 있으며, 이는 local policy로 이어질 수 있음
- (γ : 감가율, m : action의 수)

- (원인 2) Environment-noise
- 참고 논문 : Double Q-learning (Hado van Hasselt, 2010)
- environment에서 발생하는 noise는 overestimation으로 이어질 수 있음을 제안
- 이전 연구에서는 위 두가지 원인이 overestimation의 원인이라고 생각했음
- 그러나 본 연구에서 원인의 종류에 상관없이 부정확한 action value(action 평가)에 의해 overestimation이 발생한다고 주장
- 이 주장에 대한 근거로 DQN으로 Atari 게임을 학습하는 것은 function approximation이 충분히 flexible하고 환경 noise가 없음에도 불구하고 overestimation이 발생함을 제시 (실험 결과 5 참고)
<Theorem 1>
- Q*(s, a) : optimal action values // s : state, a : actuib
- V*(s) : optimal state values
- Qt(s,a) : estimate action values
- Q*(s,a) = V*(s) 가 되는 어떤 state s를 고려해보자!
- Qt(s,a)가 정확한 값이라면 아래의 수식이 성립되지만...

- Qt(s,a)에는 environment의 noise에 의해 error가 발생하는 경우가 있기 때문에 아래의 수식처럼 됨
- C : error 값 (상수)
- m : number of actions, m>=2

- Qt(s,a)에 max 연산자를 사용하면 아래와 같은 수식이 나옴

- 위와 같이 estimate value에 max 연산자를 사용하면 $\sqrt{\frac{C}{m-1}}$만큼의 bias를 가지게 됨
- 즉 optimal value에서 bias만큼 overestimate하게 됨
<Overestimate : Single Q-Learning VS Double Q-Learning (With envirionment Noise)>

- Orange Bar : Single Q-Learning's bias
- Blue Bar : Double Q-Learning's bias
- Single Q-Learing의 bias가 Dobule Q-Learing's의 bias보다 큰 것을 볼 수 있으며, 이는 action의 수가 증가할 수록 더 극대화 되는 것을 볼 수 있음
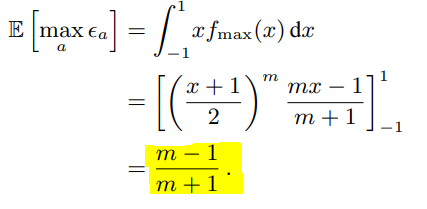
<Overestimate : Single Q-Learning VS Double Q-Learning (No envirionment Noise)>

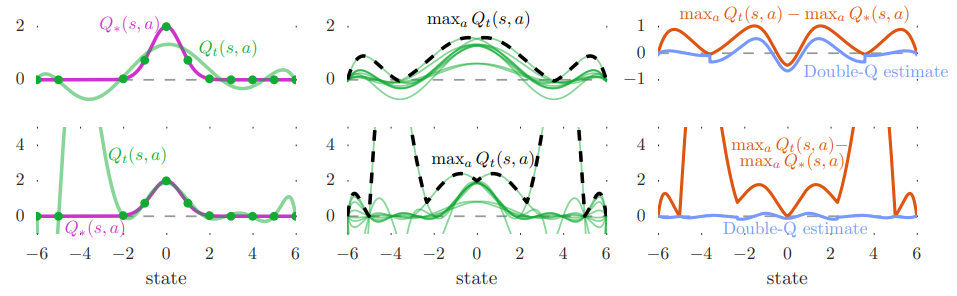
- 왼쪽 그래프 : optimal action value(보라색 선) & estimate action value(녹색 선 = approximation for a single action)
- 왼쪽 상단, 중앙의 estimate : 6차 다항식 -> green dot(sample state)을 모두 포함하지 못하기 때문에 부정확함
- 왼쪽 하단의 estimate : 9차 다항식 -> 6차 다항식에 비해 차원이 증가하여, function approximation이 충분히 flexible 해져도(green dot을 모두 포함), unsample state에서는 부정확함 -->> overestimation 문제 발생
- 중앙 그래프 : estimate action value for all action(녹색 선) & max estiamte action value(점선)
- 각각의 estimate action value 값이 다른 이유는, 서로 다른 sample state로 학습을 진행했기 때문
- Maximum estimate action value는 대부분 optimal action value 보다 값이 큼
- 오른쪽 그래프 : Bias at Single Q-Learing(주황색 선) & Bias at Double Q-Learing (청색 선)
- Single Q-Learing은 upward bias를 포함하기 때문에, 거의 항상 양의 bias 값을 가짐
- 반면에 Double Q-Learing은 거의 0에 가깝거나 Single Q-Learing에 비해 작은 bias 값을 지님
- 이는 Double Q-Learing이 overestimate를 성공적으로 줄인 것을 보여줌

- 그림 2의 상단열과 중앙열의 차이 : true value function (상단 : sin(s), 중하단 : 2exp(-s^2))
- 위 그림으로부터 overestimations은 optimal value function의 종류에 관계 없이 나타나는 것을 볼 수 있음
- 그림 2의 중앙열과 하단열의 차이 : function approximation의 flexibility
- 그림 2의 왼쪽 중앙 그래프 : 몇몇 sample state에서 estimates 값이 일치하지 않음 -> function의 flexible이 불충분함
- 그림 2의 왼쪽 하단 그래프 : 모든 sample state에서 estimates 값이 일치함 -> function의 flexible이 충분함
- 그러나! 왼쪽 하단 그래프는 unseen states에서 큰 estimation error 발생 -> 이 점이 higher overestimatioin을 발생하며, 이것이 꽤 일반적으로 일어날 수 있음을 볼 수 있음
4. DDQN : Double Deep Q Network
<DDQN 목표 및 알고리즘>
- Double Q-Learning 목표 : overestimations 감소
- Double Q-Learning 아이디어 : target Y의 max 연산자를 action의 선택(selection)과 평가(evaulation)를 분리
- action을 평가한다 = Q-Network 업데이트를 위해 action value를 가져온다
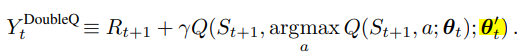

- Double Q-Learning's target Y : 두번째 네트워크의 weight로 action을 평가
- DDQN's tartget Y : target network의 weight로 action을 평가
- target network는 N episode마다 origin network(=online network)의 파라미터를 복사하는 방식으로 업데이트 (soft update)
- 즉 target network에서는 overestimate된 action value의 propagation이 기존보다 훨씬 드믈게 일어나기 때문에, overestimation 문제를 해결할 수 있음
5. Empirical Results
<Result on overoptimism>
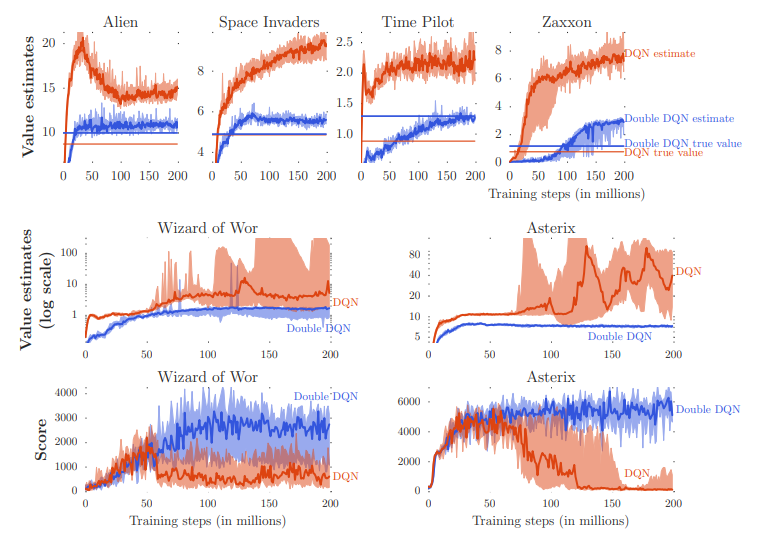
- 상단행 그래프의 주황색 그래프 및 직선 : DQN의 value estimation, true value
- 상단행 그래프의 파란색 그래프 및 직선 : Double DQN의 value estimation, true value
- DQN에 비해 Double DQN의 estimate 정도가 낮은 것을 볼 수 있음
- 또한 true value와 value estimates 사이의 차도 Double DQN이 작은 것을 볼 수 있음
- 청색 직선이 주황색 직선보다 더 높은 값을 갖는 것은 Double DQN이 더 정확한 value estimates를 할 뿐만 아니라
더 좋은 policy를 만들어 낸다는 것을 의미
- 하단행 그래프: 학습 과정 동안의 score 변화
- overestimation이 발생하면(중단행 그래프에서 value estimates이 증가하는 시점) score가 하락하는 것을 볼 수 있음
- 따라서 overestimation을 방지하는 Double DQN의 학습이 더 안정적임
<Quality of the learned policies>
- 그림 3을 통해서 overestimation을 감소하는 것은 학습의 안정성에 기여할 수 있음을 증명
- 이를 증명하기 위해 reducing overestimation에 초점을 맞춰, DQN과 DDQN은 동일한 hyper-parameter를 실험에 사용
- DQN과 DDQN의 차이 : target을 구하는 공식 (action의 선택과 평가 분리 여부)
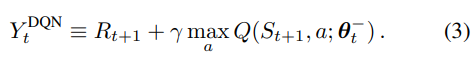

- 학습된 DQN, DDQN의 policy는 emulator 시간으로 5분(18,000 frames)동안 평가됨
- 이 때 ε-greedy policy (ε=0.05)가 적용되며, score는 100 episodes 동안의 reward의 평균 값

- 각 게임 간의 성능을 객관적으로 비교하기 위해, 아래와 같이 score 정규화 진행
- * 자세한 내용은 다음 논문 참고 : Human-Level Control throungh deep reinforcement learing (2015)

- 아래의 표 1은 DQN 보다 DDQN의 성능이 향상됐음을 볼 수 있음

- Road Runner : 233%(DQN) -> 617%(DDQN)
- Asterix : 70% -> 180%
- Zaxxon : 54% -> 111%
- Double Dunk : 17% -> 397%
<Robustness to Human starts>

6. Discussion
<본 문의 기여점>
- (1) Q-Learing에서 왜 overoptimistic이 발생하는지에 대해 증명
- (2) value estimates를 분석함으로써 이러한 overestimations이 일반적으로 발생하는 것을 증명
- (3) Double Q-Learing은 이러한 overoptimism을 줄이는데 효과적으로 사용될 수 있음을 증명
- (4) 기존 DQN 알고리즘에 추가적인 network 구조 혹은 파라미터 없이, Double DQN 이라는 새로운 아키텍쳐를 구현
- (5) DDQN은 기존의 알고리즘들보다 더 좋은 policy를 찾을 수 있으며, Atari 2600 도메인에서 state-of-the-art 달성
7. Critical Point
- overestimate의 문제를 action의 선택과 평가를 분리함으로써 해결 했는데, 문제의 원인인 env noise와 근사화 함수 사용 등에서 이러한 해결책을 어떻게 유도했을까?
- 내용 입력
