티스토리 뷰
작성자 1 : 한양대학원 융합로봇시스템학과 유승환 석사과정 (CAI LAB)
작성자 2 : 한양대학교 로봇공학과 정석훈 학부생
오늘은 optimizer 알고리즘 중 하나인 Adam에 대해 공부해보겠습니다~ 딥러닝을 학습할 때 optimizer로 SGD와 Adam을 많이 사용하지만 이 알고리즘들의 특징을 잘 모르고 사용하는 경우가 많습니다. 그래서 이번 기회에 Adam을 정리하고자 합니다! 그럼 시~작~~


- Adam 원문 링크 : arxiv.org/pdf/1412.6980.pdf
- 참고 블로그 : dalpo0814.tistory.com/29
Adam Optimizer 논문 요약/정리
Adam Optimization 논문 요약/정리 Adam Optimization 논문 요약/정리 우와… 좀더 쉽게 티스토리에 포스팅을 하기 위해 귀찮지만 노력을 들여서 evernote와 marxico, markdown의 세계에 입문하였다. 근데 marxico..
dalpo0814.tistory.com
0. ABSTRACT
(0-1) Adam이란?
- 2개의 lower-order moments의 추정치를 기반으로 stochastic object functions를 first-order gradient based로 최적화하는 알고리즘
- * lower-order moments : 번역하면 저차 모멘트인데, 2절에서 자세히 설명할 예정.
- * first-order gradient : 말 그대로 1차 함수 기울기. (1-3)에서 자세히 설명할 예정.
- * stochastic object functions : 쉽게 말하면 Loss Function이라고 보면 됩니다. mini-batch 방식과 같이 random하게 training sample을 선택함으로써 매번 loss function 값이 달라지는 함수. (MSE, Cross Entropy 등등)
(0-2) Adam의 장점
- 간단한 구현 -> 효율적인 연산 -> 메모리 요구 사항이 거의 없음
- gradient의 diagonal rescaling에 독립적 -> 파마리터(weight)마다 학습률을 달리 조정 가능!!
- 데이터 및 모델 파라미터가 많이 필요한 문제에 적합
- gradient에 noisy가 있거나, sparse(희박)한 문제에도 적합
- * 왜 적합한지는 2절 알고리즘에서 나올 예정.
- Adam의 hyper-paramter는 직관적이며, tuning이 거의 필요 없음
- * Adam의 hyper-parameter : Exponential Decay Rates (β1, β2)
- 6절의 실험 결과를 보면 Adam은 다른 stochastic optimization methods(SGD, Adagrad, RMSProp)에 비해 optimizer 성능이 좋음
(0-3) 번외
- Adam을 infinity norm 기반으로 변형한 AdaMax에 대해 논의할 예정
1. INTRODUCTION
(1-1) Object Function의 특징
- Object functions(loss function)은 stochastic(확률적)이다.
- 많은 object functions은 다른 subsample 데이터(mini-batch로 분할된 Training Data)에서 평가된 subfunctions의 합으로 구성

- 이러한 경우 mini-batch마다 gradient steps(학습으로 수정하는 gradient의 방향, 크기)을 다르게 줄 수 있기 때문에, 학습에 효율적임 -> SGD가 이에 해당
(1-2) 기존 Stochastic gradient-based optimization 알고리즘의 단점
- object function에는 noise가 발생하면 optimization의 성능이 저하됨
- 대표적인 nosie로 dropout regularization이 있음
- * dropout : 신경망의 일부 뉴런을 랜덤으로 OFF
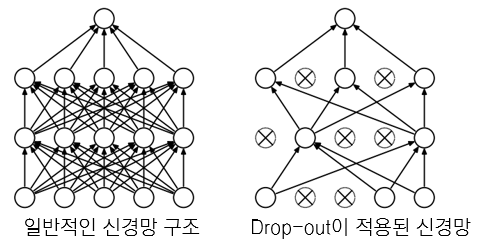
- object function에 noise가 생긴다면, 더 효율적인 stochastic optimization이 요구됨
- 본문에서는 higher-order optimization method 보다는 first-order methods로 이러한 문제를 해결하고자 함
(1-3) 추가 설명 : First-order Methods
- 참고 블로그 (1-3의 모든 사진은 이 블로그가 출처입니다.) : sunshower76.github.io/deeplearning/2020/08/22/CS231n-Lecture07/
Computer Vision, Machine & Deep Learning Blog
Computer Vision, Machine & Deep Learning Blog 설명서
sunshower76.github.io

- SGD, AdaGrad, RMSProp, Adam은 모두 First-Order Optimization
- 즉 한번 미분한 weight만 optimize에 반영됨
- 그러나 1차 함수 방향(노란색 직선)으로만 optimize하기 때문에 graident 수정이 제한적
- 이를 보완하기 위해 고차 함수 optimization(오른쪽 그림)이 등장
- 그러나 고차 함수 optimization은 역전파를 위해 역행렬을 구할 때, 시간 복잡도가 엄청나게 증가함 (ex : 가중치의 차원이 몇 백만 차원으로 늘어남)
- 이러한 이유로 아직까지는 First-Order Optimization을 사용하고 있음
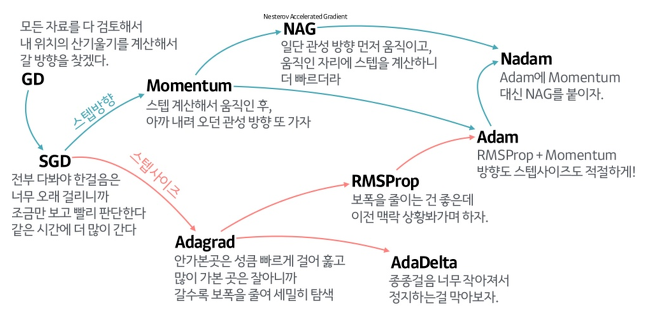
(1-4) 기존의 SG 최적화 알고리즘의 대체안 : Adam
- Adam : 적은 연산량을 지닌 first-order gradients 기반 stochastic optimization 알고리즘 -> 효율적인 알고리즘
- Adam은 gradient의 첫번째와 두번째 moment의 추정치로부터 다른 파라미터에 대한 개별적인 learing rate(학습률)을 계산
- 첫번째 moment의 추청지 : momentum optimizer
- 두번째 moment의 추정치 : AdaGrad / RMSProp optimizer
- 여담으로 Adam의 이름은 Adaptive moment estimation에서 나옴
- Adam은 AdaGrad와 RMSProp의 장점을 통합해서 디자인 됨
- AdaGrad : sparse gradient에 적합
- RMSProp : on-line, non-stationary setting에 적합 (자세한건 5절에서 설명)
5. RELATED WORK
5.2 AdaGrad
- AdaGrad : weight(가중치)의 업데이트 횟수에 따라 Learning Rate를 조절하는 옵션이 추가된 optimiziation 알고리즘
- 이러한 원리 때문에 sparse한 gradient의 최적화에도 적합함

- 업데이트가 많이 되지 않는 weight들은 Learing Rate(혹은 step size)를 크게 함 -> 적게 업데이트된 변수들은 학습률을 크게하여 빠르게 loss 값을 줄임
- 반대로 업데이트가 많이 된 weight들에 대해서는 Learing Rate를 작게함 -> 많이 업데이트된 변수는 최적값에 근접했을 것이라는 가정하에 작은 크기로 이동하면서 세밀한 값을 조정
- 위 AdaGrad 수식을 보면, weight가 많이 업데이트 될수록 h 값이 누적되고 이 역수값이 학습률과 곱해져서, 결과적으로 학습률이 작아짐

- 이러한 AdaGrad에도 단점이 존재 : 과거의 기울기를 제곱하여 계속 더해가기 때문에 학습을 진행할수록 업데이트 강도가 약해짐 -> 무한히 계속 학습할 경우에는 어느 순간 업데이트량이 0이 되어 loss 값이 더 이상 줄지 않음
- 이러한 문제를 해결하기 위해 RMSProp 알고리즘이 등장하게 됨
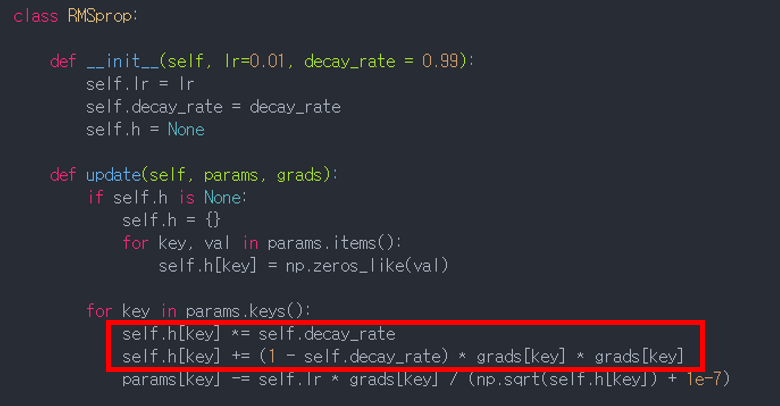
5.1 RMSProp
- AdaGrad와의 차이점 : 과거의 모든 기울기를 균일하게 더하지 않고, 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영 (이 파라미터를 decaying factor(혹은 rate)라고 부름)
2. ALGORITHM
[Adam의 Python 코드 (일부)]
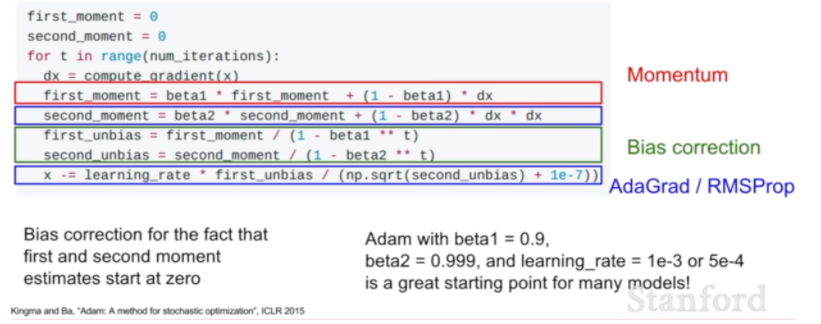
- Adam의 첫번째 moment는 Momentum 알고리즘에서, 두번째 moment는 AdaGrad/RMSProp 알고리즘에서 유도됨
- Bias Correction : 두 모멘텀이 초기에 0으로 초기화되는 문제점을 방지
[Adam ALGORITHM의 Pseudo 코드]
- adam은 크게 moment를 계산하는 부분, moment를 bias로 조정하는 부분으로 구성됨
- moment는 Momentum이 적용된 first moment와 AdaGrad, RMSProp이 적용된 second moment가 있음

[초기에 필요한 4가지 파라미터]
- Stepsize α (Learing Rate)
- Decay Rates β1, β2 : Exponential decay rates for the moment estimates (0~1 사이의 값) -> Adam의 유일한 hyper-parameter이며, gradient의 decay rate를 control 함
- Stochastic Objective Function f(θ) // θ : parameters (weights) -> f(θ) 값의 최소화가 adam의 목표
- initial Parameter Vector θ0
[Adam 알고리즘]
- (1) first & Second moment, time step 초기화
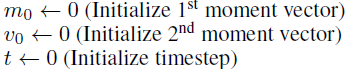
- (2) 파라미터 θ_t가 더 이상 수렴(converge)하지 않을 때 까지, 아래의 항목을 반복
- (반복문-1) time step 증가 : t <- t+1
- (반복문-2) stochastic objective funtion으로 이전 time step의 gradient 계산 (미분)

- (반복문-3) biased first & second moment 값 계산
- 위 python 코드에서 빨간색(Momentum)과 파란색(AdaGrad, RMSProp) 부분이 이에 해당
- 아래의 수식에서 β가 최신 값의 비중을 높이는 역할 (exponential decay)

- (반복문-4) 초기의 모멘텀 값이 0으로 초기화되는 경우를 방지하기 위해, bias-correction 적용
- 위 python 코드에서 초록색 부분(Bias Correction)이 이에 해당

- (반복문-5) 최종 파라미터(가중치) 업데이트
- 아래의 입실론은 0으로 나누는 일을 방지하기 위해 셋팅
- second moment가 AdaGrad, RMSProp 역할 : 파라미터의 업데이트 횟수에 따라 학습률을 달리 함 (업데이트를 많이 한 파라미터일수록 v_t 값이 커짐)

[Adam의 추가적인 설명]
- 학습률도 β로 조정하면 성능이 더 좋아짐

2.1 Adam's Update Rule
- Adam은 step size(Learning Rate)를 효과적으로 선택하는 것이 중요함
- step size는 2개의 upper bounds(상한선)가 있음 (이때는 입실론 = 0 이라고 가정)
- 효과적인 step size은 △t의 값을 최적으로 만듦

- 첫번째 case는 sparsity case 일때 적용함 (sparsity case : 하나의 gradient가 모든 time step에서 0으로 되는 경우)
- 이럴때는 step size를 크게 해서 업데이트 변화량을 크게 만들어야함 (1-B1 / 루트(1-B2)는 1보다 크므로, 학습률이 크게 됨)
- 두번째 case는 일반적인 경우 (대부분 B1 = 0.9, B2 = 0.99으로 설정하여, 1-B1 = 루트(1-B2)가 같은 값이 됨) 일 때 적용
- 이럴때는 step size를 작게 해서 업데이트 변화량을 작게 만듦
3. INITIALIZATION BIAS CORRECTION
- 이 절에서는 Bias Correction을 왜 하는지(= 각 모멘트를 1-B로 나누는 이유)에 대해서 나옴
- 수식적인 내용(E[g_t]로 변환하는 부분)을 이해 못해서... 개념적으로만 진행해보겠습니다.
- 논문에서는 second moment (v_t)에 대해서 소개함

- 우리는 second moment의 기댓값 E[v_t]를 구해야 함
- 실제로 구해야하는 참 second momet 기댓값 : E[g_t]
- E[v_t]가 E[g_t]에 근사하기 위해, 1-B를 나누게 됨
- sparse gradient의 경우, B2 값을 작게 설정함 -> 이전 time step의 기울기를 최대한 무시하게 됨
6. EXPERIMENTS
6.1 EXPERIMENT : LOGISTIC REGRESSION
[평가 데이터셋 1 : MNIST 데이터셋]

- multi-class logistic regression (L2-regularized 적용)
- * logistic regression이란? : ganghee-lee.tistory.com/29
Linear Regression vs Logistic Regression
Supervised Learning중 하나로 input data로 discrete한 값을 예측하면 Classification continuous한 값을 예측하면 Regression이라고 한다. 더 자세한 설명은 아래 이전글에서 확인할 수 있다. [딥러닝] 머신러닝..
ganghee-lee.tistory.com
- step size α는 1/√t decay로 조정됨 -> 시간에 따라 step size 감소
- logistic regression은 784 차원의 이미지 벡터로 숫자 class를 분류함
- mini batch 128로 Adam, SGD(with Nesterov), AdaGrad를 비교함 (아래 표 1의 왼쪽 그래프)
- 표1을 보면, adam은 SGD와 유사하게 수렴하고, AdaGrad 보다 빠르게 수렴하는 것을 볼 수 있음
- * x축 : 학습 횟수, y축 : loss 값

[평가 데이터셋 2 : IMDB 데이터셋]

- sparse feature problme을 테스트 하기 위해 IMDB 영화 리뷰 데이터셋으로도 adam을 평가함
- * sparse feature problem : 비슷한 유형이 적은 데이터라고 이해하고 있습니다.
- 이 데이터는 전처리가 필요 : Bow(Bag of Words) Features vector로 전처리 진행 (10,000 차원)
- * Bow Feature Vector : 문장을 벡터(숫자)로 표현
- 오버피팅을 방지하기 위해 50% 비율의 drop-out이 적용되며, 이 노이즈가 BoW Features에 적용됨
- 위 표 1의 오른쪽 그래프를 보면 loss 값이 상당히 튀는 것을 볼 수 있는데, 이것이 drop-out의 noise
- sparse한 경우 Adam, RMSProp, Adagrad는 좋은 성능을 내고 있음 (표 1의 오른쪽 그래프)
- Adam은 sparse features에서도 성능이 좋으며, SGD보다 빠른 수렴 속도를 지니고 있음
6.2 EXPERIMENT : MULTI-LAYER NEURAL NETWORKS

- multi-layer model : two fully connected hidden layer with 1000 hiden units (ReLU activation, mini-batch 128)
- Object Function : Cross-Entropy Loss (with L2 weight decay)
- * x축 : 학습 횟수, y축 : loss 값
- drop-out regularization을 적용했을 때의 optimizer 성능 비교 -> Adam이 가장 빠르게 수렴
6.3 EXPERIMENT : CONVOLUTIONAL NEURAL NETWORKS

- Convolution Neural Network : C64-C64-C128-1000
- * C64 : 64 output channel을 가지는 3*3 conv layer
- * 1000 : 1000 output을 가지는 dense layer
- 왼쪽 그래프 : 3 epoch 까지의 optimizer 별 수렴 속도 비교
- 오른쪽 그래프 : 45 epoch 까지의 optimizer 별 수렴 속도 비교
- * x축 : 학습 횟수, y축 : loss 값
- dropout을 적용하지 않은 optimizer 중에서 Adam이 제일 수렴 속도가 빠름
- dropout을 적용한 optimizer 중에서 Adam이 제일 수렴 속도가 빠름
6.4 EXPERIMENT : BIAS-CORRECTION TERM
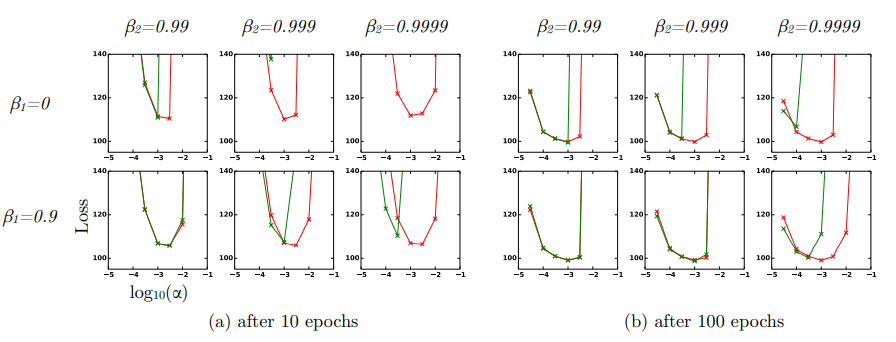
- 초록색 그래프 : no bias correction terms -> RMSProp
- 빨간색 그래프 : bias correction terms (1-B)

- Bias correction term을 적용하지 않았을 때 B2가 1.0에 가까워질수록 불안정
- 요약하자면 Adam 알고리즘은 하이퍼파라미터 설정에 상관없이 RMSProp 이상의 성능을 보였다.
7. EXTENSIONS
7.1 ADAMAX
- Adam에서 개별 weights를 업데이트 하기 위해 과거와 현재의 gradient의 L2 norm을 취함


- 이때 L2 norm을 L_p norm으로 변경할 수 있음
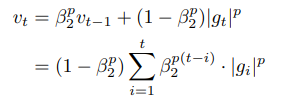
- p 값이 커질수록 수치적으로 불안정해지나, p를 무한대라고 가정(infinity norm)하면 간단하고 stable한 알고리즘이 됨

- 노란색 부분이 adam과 다른 부분이며, second moment의 수식의 변경과 Bias Correction 계산이 빠진 것을 볼 수 있음
- 그런데 L2 norm에서 Lp norm으로 확장한 것이 어떤 이점이 있는지는 모르겠음... 추가적인 공부 필요
8. CONCLUSION
- Stochastic objective function의 최적화를 위해 간단하고 효율적인 최적화 알고리즘 Adam을 소개함
- 대량의 데이터셋과 고차원의 파라미터 공간에 대한 머신러닝의 문제 해결에 집중
- Adam은 AdaGrad가 Sparse gradients를 다루는 방식(파라미터 별 step size를 다르게 적용)과 RMSProp이 non-stationary(정지하지 않는) objectives를 다루는 방식(과거의 기울기를 현재의 것보다 덜 반영함)을 조합
- Adam은 non-convex한 문제(여러 개의 최저점이 있는 문제)에서도 최적화가 잘 됨
'sinanju06 > 딥러닝 논문 리뷰' 카테고리의 다른 글
| EfficientNet : Rethinking Model Scaling for Convolutional Neural Networks 논문 리뷰 (7) | 2021.04.18 |
|---|---|
| 강화학습 논문 정리 2편 : DDPG 논문 리뷰 (Deep Deterministic Policy Gradient) (9) | 2021.03.16 |
| Focal Loss for Dense Object Detection 리뷰 (4) | 2021.02.05 |
| Mask R-CNN 리뷰 (4) | 2021.01.27 |
| 강화학습 논문 정리 1편 : DQN 논문 리뷰 (Playing Atari with Deep Reinforcement Learning) (8) | 2021.01.25 |
