티스토리 뷰
강화학습 논문 정리 5편 : CQL 논문 리뷰 (Conservative Q-Learning for Offline Reinforcement Learning) (업데이트 중)
hanyangrobot 2021. 8. 10. 11:31작성자 : 한양대학원 융합로봇시스템학과 유승환 석사과정 (CAI LAB)
안녕하세요~!! 오늘은 오프라인 강화학습 알고리즘 중 하나인 CQL : Conservative Q-Learning의 논문 리뷰를 진행하겠습니다! 'Conservative'의 뜻은 '보수적'이라는 뜻을 지니고 있는데요~ 이 의미가 어떻게 CQL 알고리즘에 표현되는지를 보겠습니다!! 실제 다관절 로봇에 강화학습을 적용하려는 저와 같은 연구자분들은 기존의 강화학습(ex : Off-Policy RL)을 사용하려면 Experience Replay Buffer에 수많은 데이터를 쌓아야해서, 데이터 수집 비용이 비싸다는 한계점이 있었는데, 이를 어떻게 극복했는지를 한번 알아보겠습니다~!
1. 원문 링크 : https://arxiv.org/abs/2006.04779
Conservative Q-Learning for Offline Reinforcement Learning
Effectively leveraging large, previously collected datasets in reinforcement learning (RL) is a key challenge for large-scale real-world applications. Offline RL algorithms promise to learn effective policies from previously-collected, static datasets with
arxiv.org
2. 깃헙 링크 : https://github.com/aviralkumar2907/CQL
GitHub - aviralkumar2907/CQL: Code for conservative Q-learning
Code for conservative Q-learning . Contribute to aviralkumar2907/CQL development by creating an account on GitHub.
github.com
1. Introduction
(1-1) 온라인 강화학습의 장점과 단점
- 최근 온라인 강화학습은 Deep Neural Network로 Q-function을 근사화함으로써 많은 진보가 있었음
- 특히 Robotics[31], Strategy Games[4] 그리고 Recommendation System[37] 분야에서 뛰어난 성과가 나오고 있음

- 그러나 온라인 강화학습을 현실 세계에 적용하는 것은 실용적인 어려움이 존재
- 온라인 강화학습은 각 학습 과정마다 활동적인 환경 상호작용이 필요한 active learning process가 전통적으로 여겨지기 때문
- 실제 세계와의 상호작용은 비용이 들고 위험할 수 있음
- 온라인으로 수집할 수 있는 데이터 양은 지도학습에서 사용되는 오프라인 데이터셋보다 상당히 적음.
(1-2) 오프라인 강화학습의 장점과 단점
- 이를 보완할 수 있는 대안책 : 오프라인 강화학습(offline Reinforcement Learning)
- 오프라인 강화학습은 환경과의 상호작용 없이, 대규모로 수집된 데이터셋에서 학습됨
- 실제 세계와의 상호작용이 없기 때문에 비용이 없고 안전함
- 지도학습에서 사용되는 오프라인 데이터셋만큼 대량으로 수집할 수 있음
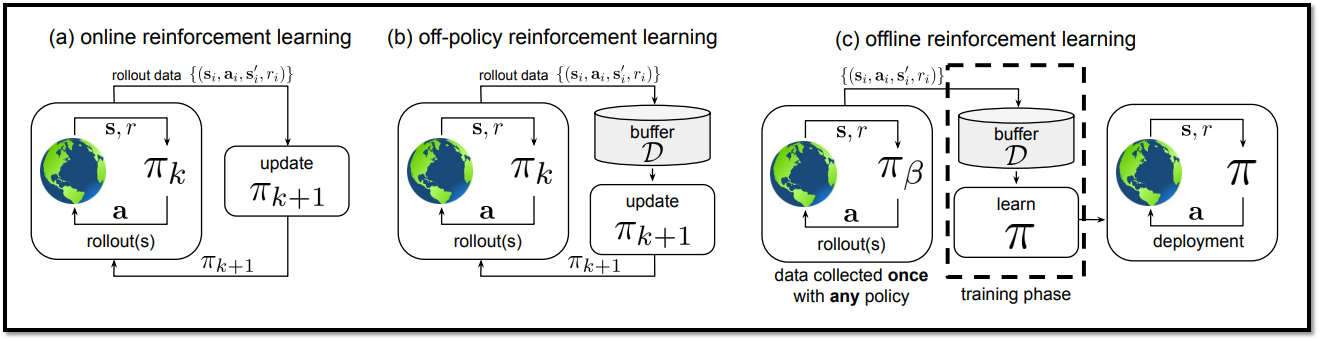
- 그러나 오프라인 강화학습은 데이터를 수집한 정책과 학습된 정책 간의 분포 변화(Distributional Shift)에서 비롯된 주요 기술적 어려움을 겪고 있음
- 강화학습은 기본적으로 TD(Temporal Difference) 방식을 기반으로 가치 함수를 업데이트함 : $TD_loss = r_{t} + \gamma argmax_{a_{t+1}}Q(s_{t+1}, a_{t+1})-Q(s_t, a_t)$
- 이때 다음 타임 스텝 $t+1$의 행동 $a_{t+1}$을 선택하기 위해서 argmax 연산을 사용함.
- 이렇게 선택된 $a_{t+1}$은 unseen actions일 수 있음
- 온라인 강화학습은 중간에 학습된 정책과 환경 간의 상호작용을 통해 다양한 데이터를 수집할 수 있지만, 오프라인 강화학습은 그렇지 못하기에 argmax 연산에 의해 unseen actions을 과대평가 할 수 있음.
- 즉 기존의 value-based off-policy 강화학습 알고리즘을 오프라인 환경에서 직접 활용하는 것은 일반적으로 "out-of-distribution actions(= unseen actions)에서의 부트스트래핑 문제 및 오버피팅과 관련된 문제"로 인해 성능이 저조하며, 이는 잘못된 낙관적(optimistic) 가치 함수의 추정으로 나타남.
(2) 제안하는 방법론 : 보수적인 가치 함수의 학습
- 연구 가설 : 가치 함수의 보수적인 추정을 학습할 수 있다면, Q 값의 과대 추정 문제를 해결할 수 있을까?
- 제안하는 방법 : 일반적은 가치 기반 강화학습 알고리즘에 간단한 수정을 통해 보수적인(conservative) Q 함수를 학습하기 위한 혁신적인 방법을 제안
- 핵심 아이디어 : (상태-행동) 데이터에 대한 적절한 분포 아래에서 Q-값을 최소화하고, 이를 데이터 분포에 대한 최대화 항과 결합하여 이 경계를 더 강화하는 것.
(3) 연구의 기여점
- 주요 기여점 : 학습 도중에 Q 값을 규제하여 가치 함수의 보수적이고 하한 추정치를 학습하는 알고리즘적 프레임워크를 제안 -> "Conservative Q-Learning (CQL)" 이라고 부름
- 이론적 분석 : 정책의 분포 아래에 있는 Q 함수의 기대 값만이 실제 정책 값의 하한을 설정하며, point-wise lower-bounded Q 함수로 인해 발생할 수 있는 추가 하한 과소평가를 방지함
- 실험적 분석 : 실험 결과를 통해 Q 함수 추정 오차에 대한 CQL의 견고성을 증명함
- 쉬운 구현 : 기존 강화학습 알고리즘에 20줄 내외의 CQL loss term을 추가함으로써 CQL을 쉽게 구현 가능
- CQL은 다양한 벤치마크 작업에서 이전 방법들보다 2-5배 이상 뛰어난 성능을 보임
- 이는 사람과의 상호작용에서 수집한 실제 데이터셋 중 일부에서 간단한 behavior cloning 기법을 능가하는 유일한 방법임
2. Perliminaries
(1) 온라인 강화학습
- 강화학습의 목표 : MDP(Markov Decision Process)에서 누적된 reward의 기댓값을 가장 극대화하는 policy를 학습하는 것
- MDP 구성 : tuple -> (State, Action, Dynamic, Reward, Discount factor)
- * Dynamic Function : Next_State로 갈 확률 분포


- Behavior Policy, πβ(a|s) : Offline 데이터 수집에 사용되는 policy
- Discounted Margnial State-Distribution of Behavior policy, dπβ(s) : policy π를 따랐을 때의 state 확률 분포
- D : Dataset

- 모든 state는 Dataset D에 포함됨
- empirical behavior policy, ^πβ(a|s) : state s에서 action a를 할 확률
- r(s,a)는 정의한 R_max 값보다 크지 않음

<Off-Policy & Actor-Critic 개요>
- Off-policy RL은 파라미터화된 Q함수와 policy를 포함
- * Actor-Critic의 경우, Q함수 : Critic Network, Policy : Actor Network
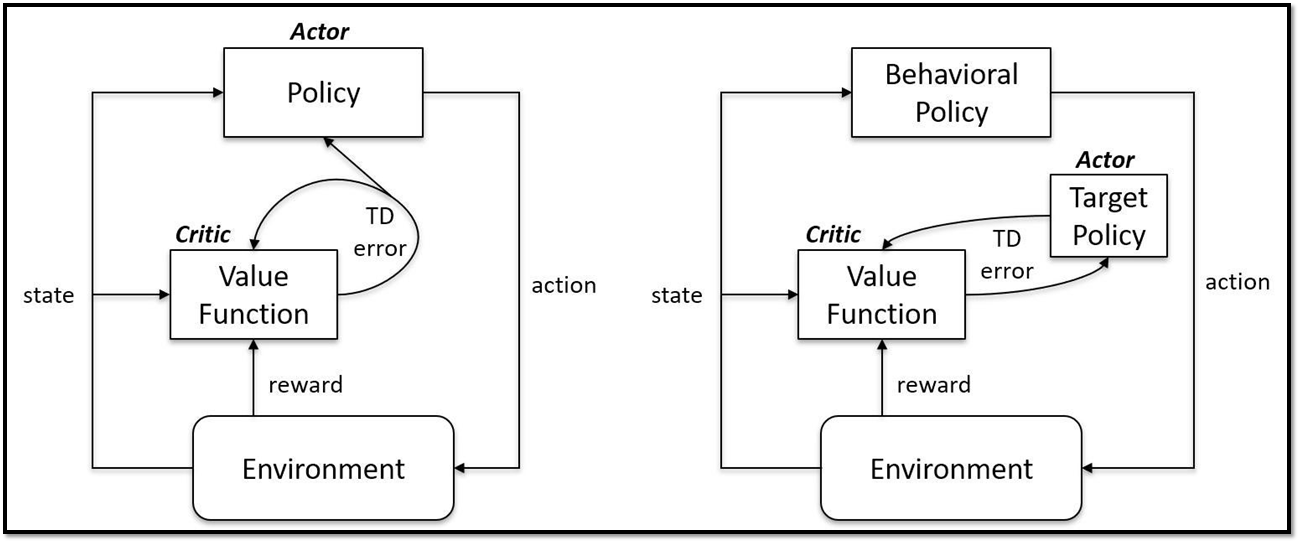
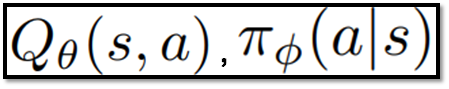
- Q Learning의 학습 과정 : Bellman optimality operator와 True Q-Value의 차이를 파리미터에 업데이트하는 것을 반복 적용

- Q-vlaue의 기댓값이 최대화 되는 action을 향하도록 policy를 improve 및 evaluation

<Offline RL 개요>
- Off-policy를 기반으로 한 Offline RL 알고리즘들은 학습 도중 action distribution shift 문제 발생
- action distribution shift 원인 : policy evaluation에서 estimate Q-function, ^Q(s, a)는 learned policy π_k에서 sample된 action을 사용하지만, True Q-function, Q(s,a)은 오로지 dataset D를 수집할 때 사용하는 behavior policy π_b, 즉 데이터셋에서 sample된 action을 사용 -> Dataset에 없는 action에 대해 평가해야 하는 경우 발생

- policy는 Q-value를 극대화하는 방향으로 학습되기 때문에, 본적 없는 action들은 높은 Q-value로 out-of-distribution actions으로 편향될 가능성이 큼
- 이 원인은 데이터를 수집하는 behavior policy π_b와 Q-function 값을 예측하는 learned policy π_k가 분리되어 있기 때문에 발생하므로, 하나의 policy로 합쳐서 모든 데이터 수집 및 학습을 실제 환경에서 action을 시도하고 실제 값을 관찰하면 이러한 error를 수정할 수 있음
- 하지만 환경과의 상호작용은 비용이 많이 들고 위험하기 때문에 거의 불가능하므로, Offline RL에서 OOD (out of distribution) action에 대한 Q-value 수정이 어려움 (policy를 합치는건 Offline RL을 사용하는 목적이 사라지는 것이기도 함...)
- 전형적인 offline RL 알고리즘은 learned policy π_k에 제약을 걸어서 이 문제를 완화시킴
- 그러나 근본적인 원인을 기반으로 제시한 해결책이 아니므로, 실제 환경에서 test를 할 때 state distribution shift 문제가 발생할 수 있으며, π_k의 true 값 기준을 측정하는 estimator를 추가 생성해야해서 알고리즘이 복잡해짐
3. The Conservative Q-Learning (CQL) Framework
3.1 Conservative Off-Policy Evaluation
<목표에 대한 개요>
- 목표 : Value Function인 Vπ(s)의 값(state s에 대한 기댓값)을 예측하는 것
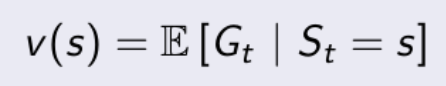

- Vπ(s) : behavior policy π_β(a|s)에 의해 생성되는 데이터셋 D에 의해 학습되는 Learned policy π_k의 Value Function
- 본 연구의 관심사 : overestimation 현상을 방지
- 해결책 : standard Bellman error objective에서 out-of-distribution action들의 Q-values를 최소화함으로써 conservative, lower-bound Q-function을 학습 -> OOD action의 Q-value에 대한 규제화 필요 (regularization 혹은 penalty)
<아이디어 구체화 1 : Objectives for Q-function training -> lower bounds Q-value>
- 핵심 아이디어 : state-action 쌍인 µ(s,a)의 특정 distribution, 그 중에서 Dataset D에 없는 action도 포함하는 Q-function을 계산하는데, 이에 대한 Q-function 값을 최소화시킴 (수식 1의 빨간 박스 영역)
- μ(a|s) : 데이터셋에 있는 state를 input으로 받고 action을 output으로 내는데, 이 때의 action은 데이터셋이 속하지 않은 action일 수도 있음
- 수식 1의 빨간 박스 영역은 trade off 계수 α로 값의 영향력을 조절할 수 있으며(아래 수식 1의 빨간 박스), α가 충분히 크면 모든 state, action에 대해 ^Qπ(s, a) <= Qπ(s,a)를 만족
- 이에 대한 증명은 Theorem 3.1에서 볼 수 있음



<아이디어 구체화 2 : Value Function에 집중>
- Action-value Function, Q(s, a) 대신 Value Function, Vπ(s)의 estimate하는 것에 집중한다면, lower-bounds : ^Qπ <= Qπ 를 더 좋게 개선할 수 있음
- 수식 (2)의 빨간 부분 같이, Q-value maximization term을 추가
- Q-value maximization term의 특징은 data distribution인 ^πβ(a|s)의 범위에서 존재
- 파란색 영역을 최소화하는 Q 값을 찾아야 하는데, 파란색 영역 중 왼쪽 기댓값은 Dataset에 없는 action에 대해서도 Q-function을 계산하기 때문에 overestimate 경향 존재 -> 이에 따라 오른쪽 기댓값(Offline 데이터 수집에 사용하는 behavior policy에 속하는 action을 사용)도 값이 커져야 파란색 영역을 최소화할 수 있으므로, 오른쪽 기댓값(빨간 글씨)을 maximize하게 됨
- 이로써 µ(s,a) = π(a|s)일 때, ^Vπ(s) <= Vπ(s)를 보장할 수 있음 (^Qπ <= Qπ는 보장하지 못하지만!)
- * 이때의 policy는 learned policy 같지만... 논문에 정확한 언급이 없네요 ㅜㅜ
- 이에 대한 증명은 Theorem 3.2에서 확인 가능



<In summary>
- 수식 (1) - basic CQL evaluation : Qπ(a,s)(true Q-function)보다 작은 값을 지니는 ^Qπ(a,s)(estimate Q-function) 학습
- 수식 (2) - variations CQL evaluation : Vπ(s)(true Value-functnon)보다 작은 값을 지니는 ^Vπ(estimate Value-function) 학습
- trade off 계수 α : 적합한 α의 경우, 위 수식 1,2의 lower bounds를 항상 보장
3.2 Conservative Q-Learning for Offline RL
<아이디어 구체화 3 : Conservative Q-function for Policy Improvement>
- 기존 수식 1, 2(Off-Policy)를 Offline RL에 적용하는데 발생하는 한계점 : policy의 최적화를 위해 policy evaluation(target policy or Critic Network)와 policy improvement(behavior policy or Actor Network)를 번갈아가며 연산하기 때문에, Policy Optimization의 연산량이 너무 큼
- Optimization 해결책 : policy evaluation과 improvement를 한번에 진행하기 -> policy ^π_k는 Q-function에서 유도되기 때문에, policy improvement는 현재 Q-function 값을 최대화하는 policy를 근사화할 수 있는 µ(s,a)를 선택하면 됨 (max µ)
- 수식 (3)에서 R(µ)이라는 regularizer를 추가함으로써 CQL(R)이라고 명명함
- R(µ)의 종류에 따라 CQL 특성이 변화하며, 이에 대한 내용은 <CQL Variants>에서 설명 예정
- CQL은 Q-learning 알고리즘 뿐만 아니라 Actor-Critic 알고리즘에도 적용 가능
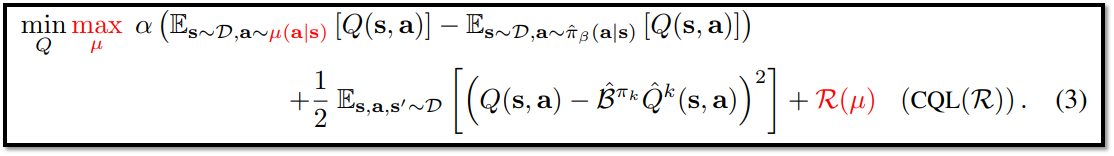

- Theorem 3.3을 통해 CQL은 모든 state에 대해 ^V(s) <= V(s) 임을 증명
- learned policy(^π_k+1)와 optimal policy(π_^Qk)가 같으면, Theorem 3.3의 LHS(D_tv(^π_k+1, π_^Qk))은 CQL update의 k+1번째의 ^V_k+1의 값에서 발생한 conservatism 값과 같음
- * D_tv : Total Variation Divergence

- 그러나 learned policy와 optimial policy는 다를 수도 있기 때문에, RHS(ε)는 두 policy의 차이로 인해 발생하는 overestimate의 최댓값으로 볼 수 있음
- lower bound를 얻기 위해서, underestimation 값이 커야 하는데, 이는 ε를 작을 경우, 즉 policy가 천천히 변경되어야 함

- 마지막으로 CQL의 Q-function이 "gap-expanding" 하게 업데이트 됨을 보여줌
- Gap-Expanding : PDataset에 있는 action(In distribution action)의 Q-value와 Dataset에 없는 action(Out of distribution action)의 Q-value의 차이가 Predict Q-function이 True Q-function 보다 해당하는 차이보다 큰 경우를 의미
- 이것은 policy π_k(a|s)가 dataset distribution πˆβ(a|s)에 더 가까워지도록 하는 것을 의미함
- 따라서 CQL update는 Offline RL에서 주요 관심사였던 OOD action과 distribution Shift 문제를 방지할 수 있음
- 만약에 sampling 오류로 인해 OOD action가 발생하고, 이에 따라 학습된 Q-value보다 높아지면, in-distribution actions을 선호하는 Q-value를 사용하여 policy가 업데이트된다는 점에서, CQL backups은 보다 robust해질 것이라고 예상됨

<CQL Variants>
- 유형 (1) : CQL(H)
- R(µ)를 H(µ)로 설정하고 풀이한 결과가 수식 (4).

- 유형 (2) : CQL(ρ)
- R(µ) 대신 KL-divergence regularizer로 설정하고 풀이한 결과가 수식 (7)
- CQL(ρ)는 고차원 action space에서 더 안정적으로 수렴하며, 이에 대한 분석은 6.Experimental Evaluation의 Table 2에서 진행할 예정.


<In summary>
- (1) CQL RL 알고리즘은 충분한 α값과 함께 Q-value의 lower-bound를 학습할 수 있음
- -> 이는 final policy가 최소 estimated value를 얻을 수 있음을 의미함
- (2) CQL Q-function이 Gap-Expanding임을 보여줌
- -> 이는 in-distribution action과 out-of-distribution actions 간의 gap을 over-estimate하여 OOD action을 방지해야 함
3.3 Safe Policy Improvement Guarantess
<Provide a safe policy improvement result for CQL>
- empirical return of any policy π, J(π, ^M) : Dataset D에 의 해 관찰된 transitions(s, a, r, s')에 의해 생성된 emprical MDP, ^M에 대한 policy π의 discounted return을 의미
- J(π, M) : actual underlying MDP, M에 대한 policy π의 discounted return을 의미

- Theorem 3.5은 CQL이 RL empirical objective의 최적화 과정을 보여줌 (파라미터 업데이트)
- 또한 D_cql에 의존하는 penalty를 통해 learned policy π이 behavior policy ^πβ와 크게 차이 나지 않는 것을 보장함

- * Learned Policy와 Behavior Policy가 다르면 D_CQL 값은 양수가 됨 -> 이 값이 J(π, ^M) 즉 기댓값에서 빠지게 되므로, 두 policy가 같아지도록 학습하게 됨

<In summary>
- (1) CQL은 penalized empirical RL objective를 최적화하며, high-confidence safe policy improvement를 보장함
4. Practical Algorithm and Implementation Details
- CQL 알고리즘은 두 유형을 기반으로 만듦 : Q-learning & Actor-Critic -> Discrete & Continuous Domain을 모두 고려함
- Q-Learning은 DQN(Deep Q Network)을 참고했고, Actor-Critic은 SAC(Soft Actor Critic)를 참고함
- 모델 학습하는데 CQL(H)를 사용
- CQL은 이전 Offline RL 알고리즘에서 사용했던 policy constraint를 사용하지 않음
- 따라서 추가적인 behavior estimator를 설정할 필요가 없어서, 본 알고리즘은 간단해짐
- α 값은 Discrete control에서는 고정했고, Continuous Control에서는 Lagrangian Dual Gradient Descent를 통해 자동으로 조절함

6. Experimental Evaluation
<실험 개요>
- CQL 모델 1 : actor-critic CQL, using CQL(H)
- CQL 모델 1의 데이터셋 : continuous control datasets from the D4RL benchmark
- CQL 모델 1과 비교한 이전 offline RL 모델들 : BEAR, BRAC, SAC, BC

<Gym domains : Continuous Control by actor-critic CQL>


- CQL(H)는 BEAR, BRAC, SAC 그리고 BC와 같은 prior methods와 유사하거나 더 좋은 성능(game score)을 냈으며, 특히 난이도가 mix된 (mixed, meduim-expert, random-expert) 도메인에서 prior method보다 2~3배 더 높은 성능을 달성하면서 robust함을 증명
<AntMaze, Adroit, Kitchen : Continuous Control by actor-critic CQL>


- Antmaze : medium, large task에서 prior methods는 모두 점수가 0인데, CQL만 유일하게 0이 아닌 점수를 얻음
- Adroit tasks : 24 자유도의 로봇 손 제어로 인해 action space 차원이 매우 높으나, CQL이 prior methods 중에서 가장 성능이 좋음 & CQL(H)보다 CQL(ρ = ^π_k−1)이 더 높은 성능을 보이는데, 고차원의 action space에 대한 해석이 뛰어난 것으로 보임
- Kitchen : 9자유도의 로봇 머니퓰레이터 제어를 해야 하며, 역시 CQL 성능이 가장 뛰어남
<Offline RL on Atari games : Q-Learning>


- Discrete Domain에서 역시, CQL이 prior methods와 성능이 비슷하거나 더 높은 것을 확인할 수 있음
<Analysis of CQL>

- CQL의 Predict Policy Value는 True Policy Value보다 작음을 보여줌으로써, Theorem 3.2를 실험 결과로써 증명함
- CQL(H)는 CQL(Eq 1)보다 덜 적게 conservative함
7. Discussion
- 본 연구에서는 Conservative Q-Learning(CQL) : policy value보다 lower bound를 배우는 offline RL을 위한 알고리즘 프레임워크를 제안함
- 본 실험 결과에서 CQL이 복잡한 제어와 raw image observation을 포함한 광범위한 offline RL task에서 기존 방법들을 능가하는 것을 보여줌
- CQL의 단순성과 효율성은 광범위한 실세계 offline RL 문제에 대해 좋은 선택임
- 그러나 아직 여러가지 문제가 남아 있음
- 문제 (1) : 선형 및 비선형 함수 근사 사례의 부분 집합에서 Q 함수에 대한 하한을 학습한다는 것을 증명하지만, Deep Neural Networks를 갖춘 CQL에 대한 이론 분석은 향후 연구를 위해 남겨져 있음
- 문제 (2) : Offline RL 방법은 지도 학습과 같은 방식이기 때문에 over fitting 문제가 발생할 수 있으므로, 지도 학습에서 사용되는 early stopping 방법과 같이 효과적인 조기 중지 방법을 고안해야 함
