티스토리 뷰
#제어이론 #제어공학 #제어 #임피던스제어 #로봇공학
"Simple" Impedance Control
원시적인 임피던스 컨트롤 적용은 Hogan에 의해서 1985년도에 제시 됐는데 꽤 성공적으로 적용됐다. 여기서 "Simple"은 힘이나 토크 제어가 되는 엑추에이터로 본질적으로 적은 마찰력을 가지는 매커니즘으로 이루어져있다는 뜻이며, output 임피던스를 증가시키려고 모션 피드백을 사용한다. 이 방식은 매커니즘에서 오는 물리적인 임피던스를 보상하려는 일은 하지 않는다. 따라서 실제 output 임피던스은 매커니즘에서 오는 컨트롤러 펄스로 구성되어 있다.
만약 댐핑과 엑추에이터, 환경에 의한 토크로 구성된 다 자유도 로봇을 모델링하게 되면 로봇의 simple impedence controller는 아래와 같을 것이다. (If a robot is modeled as a multi-degree-of-freedom inertia retarded by damping and subject to actuator and enviromental torques, the robot with the simple impedance controller is as follow)

이때 세타는 로봇의 조인트 변수를 뜻한다. I의 경우 로봇의 이노시아 매트릭스인데 로봇의 자세에 따라 달라진다. C는 코리올리와 centrifugal accelrations(초과 원심 가속도)에 의한 비선형 이노시아 커플링 토크를 뜻한다. D는 감소하는 속도와 연관이 있는 토크(마찰력)의 벡터를 말한다.
Ta는 액추에이터 토크 벡터, Te는 환경에서 의한 토크 벡터이다.
원하는 행동(behavior)은 임피던스로, 만약 스프링 매트릭스 Kj와 댐퍼 매트릭스 Bj의 행동을 선택했다면, 컨트롤 법칙(control law)는 단순히 아래와 같다.

결국 선택한 K와 B의 값에 따라 엑추에이터가 만들어야하는 토크 벡터를 표현하는 식이다.
이때 세타0은 joint space에서 Virtual trajectory를 뜻한다. 로봇 다이나믹 식과 컨트롤러의 임피던스 식을 합치면 아래와 같아진다.
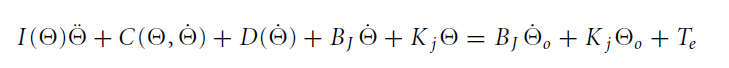

이 컨트롤러는 위 사진과 같은 동작을 로봇 Joint space에서 구현한다. 컨트롤러의 스프링과 댐퍼는 virtual trajectory로 지정된 방향으로 로봇 포즈를 밀거나 당기거나 한다.
일반적인 로봇의 비선형 운동학으로 인해서 포즈(pose)에 따라 변하는 로봇팔 끝단부(end-effector)의 stiffness와 damping을 위 식에서는 단순히 상수값으로 취급하게 된다. 하지만 이런식으로 위 식을 정의하는 것은 로봇 Joint space에서 로봇의 운동학 매트릭스를 사용해 끝단부의 임피던스를 제어할 수 있게 된다.
순기구학(Forward Kinematic equations)식 (X=L(theta))과 pose-dependent한 transformation의 자코비안(X' = J(theta)*theat')식과
액추에이터 토크에 로봇 끝단부의 force (Fe) 관한 식이 필요하다. 로봇 조인트 변수에 대해서 로봇 액추에이터가 독립적으로 동작한다고 했을 때 일반적인 표현 방식을 위해 필요한 transformation은 자코비안의 전치 행렬이다. Ta = Transpose(J)(theta)*Fe
로봇 끝단부의 상수 stiffness K와 damping B에 대한 target 임피던스를 얻기 위한 제어 식은 아래와 같다.

이 식은 위에 나왔던 Ta 식의 비선형으로 대응되는 식이다. 여기서 중요한 점은 자코비안의 rank가 줄어든다 해도 필요한 비선형 변환이 로봇 워크스페이스 전반에서(throughout) 잘 정의되도록 보장되어 있다는 것이다. 따라서 simple 임피던스 컨트롤러가 로봇의 운동학적 싱귤러리티에서 혹은 그 가까이에서 움직일 수 있게 된다.
한가지 알아야할 점은 simple 임피던스 컨트롤러는 힘 센서나 힘 피드백에 의존하지 않는 다는 점이다. 만약 로봇의 이노시아나 마찰에 대한 힘이 충분히 작다면, 로봇의 interaction port(주로 로봇 끝단부)의 행동은 원했던 임피던스와 비슷할 것이다. Inertial forces(관성력)은 느린 움직임에서 줄어들고 로봇이 정지하게 되면 사라진다. 이런 이유로 simple 임피던스 컨트롤러는 몇가지 어플리케이션에 꽤 효율적일 수 있다. 마찰에 의한 힘도 느린 움직임에 감소하게 되는데 실제로 로봇이 멈춰도 완전히 사라질 필요는 없다. 이런 이유로 낮은 임피던스를 요구하는 interactive robot 설계에서 낮은 이노시아와 마찰력이 필요한 이유이다. (...?)
컨트롤러 디자인 관점에서, simple 임피던스 컨트롤 제어 식인 아래식은 Joint space에서의 가상의 경로(virtual trajectory)와 실제 경로의 차이에 대한 PD 컨트롤러와 비슷하다. 로봇을 컨트롤 가능한 힘으로 움직이는 질량이라고 가정할 때, 임피던스 컨트롤러의 stiffness K와 damping B는 PD 게인과 상응한다.
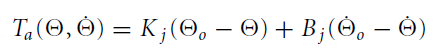
simple 임피던스 컨트롤러의 비선형 형태인 아래 식은 gain-scheduled PD 모션 컨트롤러와 비슷하다. 이때는 비선형 변형이 로봇 끝단부의 일정한 움직임을 만들기 위해 P와 D gain을 바꾸는 형태이다.

중간에 도대체 뭔소리야? 하는 부분이 있었지만 어느정도 새로운 사실을 알아갔다. 실제 임피던스 컨트롤러를 왜 PD 컨트롤러와 동일하게 보는지에 대한 내용도 알게되어서 좋다. PDF에는 그 이외에 임피던스 컨트롤러가 좋은 이유에 대해 설명하고 있지만 이 부분은 스킵하도록 하자. 물론 제일 마지막에 한계점도 말한다.
한계점에 대해서와 그 한계점을 극복하는 방법에 대해서 다음글에 다루겠다.
'미니멀공대생 > Control' 카테고리의 다른 글
| Multiobjective Optimization for stiffness and position control in a soft robot arm module (4) | 2021.07.26 |
|---|---|
| [강화학습] Dynamic programming (0) | 2021.06.04 |
| [Null space control] Null space control이란? (8) | 2021.05.18 |
| [Null space control] Nullspace에 대하여 (2) | 2021.05.18 |
| [임피던스 제어] Interaction Control 적용 - Virtual Trajectory & nodic impedance (4) | 2021.05.14 |
