티스토리 뷰
[논문리뷰] Mobile manipulation in unknown environmets with differential inverse kinematics Control
미니멀공대생 2022. 2. 27. 00:28Mobile manipulation in unknown environmets with
differential inverse kinematics Control
저자 : Adam Heins, Michael Jakob, and Angela P.Schoeling
논문 : https://ieeexplore.ieee.org/document/9469430
작성 : 이해구
개인적인 공부를 위해 작성하는 논문 리뷰입니다. 완변학 이해 없이 읽으면서 작성하였기 때문에 이상한 부분들이 많습니다. 댓글에 저보다 잘하시는 분들이 틀린점을 수정해주실 수 있으니, 댓글을 봐주시면 더 좋을 수도 있습니다
ABSTRACT
모바일 매니퓰레이터는 모바일 로봇의 넓은 워크스페이스와 로봇 팔의 상호작용을 합쳐서 다양한 분야에 사용될 수 있는 가능성이 있다. 논문에서는 differential Inverse Kinematics(DIK) whole body control 방식의 위치 제어 기반 모바일 매니퓰레이터를 다룬다. 논문에서 제시한 제어기는 task space에서 경로 추정, force regulation, 장애물과 싱귤러리티 회피 그리고 외부 환경에 대한 데이터가 부족한 상황에서도 물체를 밀어 원하는 위치 까지 가는 작업들이 가능하다. 논문에서는 총 9자유도(3+6) 로봇을 사용하였다.
INTRODUCTION
논문에서는 Whole-body control 접근을 통해 역미분기구학 (Differntial Inverse Kinematics) 기반인 위치 제어기를 이야기 한다. 기존 방식과 논문에서 언급하는 방식을 비교해보자.
Motion planning 방식
- 분명하고 순차적이며 실행 단계가 있는 방식.
- Sequnetial planning and execution phases
Control level에서의 방식
- 빠르게 들어오는 외부 힘에 대해서 빠르게 반응할 수 있다.
이를 보이기 위해, task space에서의 경로 추적, 힘 제어, 장애물과 싱귤러 피하기에 대해 이야기를 먼저 한다.
RELATED WORK

논문에서의 주된 목적은 로봇의 역기구학을 푸는 것이다. 일반적으로 속도 레벨에서 (differential) IK문제를 푸는데, 시스템이 redundant system(여자유도 시스템)일 경우 이에 대한 해는 analytical least squares 방식으로 구할 수 있다. 이런 redundancy resolution 방법들로 아래와 같은 것들이 있다.
- Extended Gradient
- Projected Gradient
- Reduced Gardient
Differential inverse kinematic와 Quadratic programming
하지만 이런 방법들은 조인트의 위치나 속도 제한이나 장애물 회피, field of view 제약과 같은 ineqaulity constraints를 만족시키지 못한다. (참고논문) inequality constraints는 DIK 방식을 일반적인 quadratic programming(QP)로 접근하여 푸는 걸로 해결할 수 있다. 이 방식이 논문에서 근간으로 가져가는 방식이다.
여자유도의 파라미터화의 장점과 단점
여자유도를 사용하는 방법으로는 모바일 로봇과 로봇 팔의 기하학적 관계를 설명하는 여자유도 파라미터를 정의하는 방법이 있다. 이런 파라미터들을 online 최적화 문제로 두고 푸는 방법이다. 이런 방식은 여자유도를 설명 가능하게 표현할 수 있다는 장점이 있지만, 실제로는 여자유도 파라미터를 설정하기가 쉽지 않다.
여자유도 시스템
1. 다수의 Task를 동시에 완료할 수 있다.
- 우선순위가 높은 Task를 먼저 수행될 수 있도록 순위가 낮은 Task를 우선순위 Task의 Null space에 빼는 방식으로 계층적 우선순위 제어 프레임워크를 만든 형태의 연구가 있다.
2. 계층적 Task quadratic programming
- 각 Task를 하나의 QP로 표현하고, 낮은 우선순위의 QP해가 높은 우선순위의 QP의 해에 포함될 수 있도록 제약(Constriant)을 거는 형태로 진행할 수 있다. [참고눈문]
논문에서 싱귤러+장애물 회피의 방법으로 채택한 것이 계층적 Task QP 방식이다.
또한 다수의 논문이 MPC를 통해서 Task space 상에서 작업을 진행했는데, 논문에서는 조금 간단하고 계산이 적은 DIK 기반으로 진행을 했다.
SYSTEM MODEL

6자유도 + 3자유도, 총 9 자유도를 가진 로봇으로 조인트 정보와 입력값을 아래 식과 같이 표현할 수 있다.
또한 이를 이용한 이산화 모션 모델도 표현 할 수 있다.
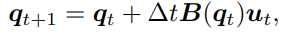
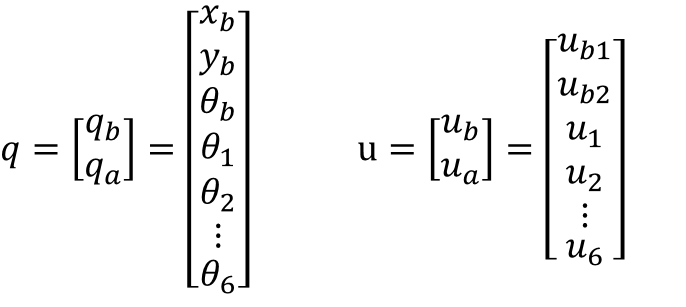
여기서 B는 경우 입력값 U를 속도로 매핑해주는 매핑 행렬이며 아래와 같이 표현할 수 있다.
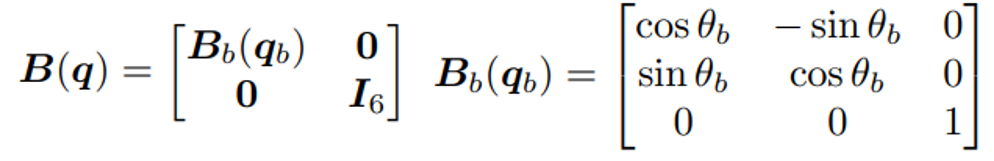
METHODOLOGY
논문에서는 조인트와 데카르트 상에서의 속도를 선형적으로 매핑해주는 형태의 DIK 방식을 사용한다.
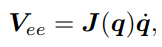
여기서 Vee의 경우 spatial twist이며 선속도와 각속도로 이루어져있다. geometric jacobian 행렬의 경우 6x9 크기를 가진다. B 행렬을 이용해서 선형 매핑식을 정리하게 되면 아래와 같다.
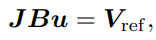
Vref의 경우 EE(End effector)가 따라야 하는 twist를 말한다. 논문에서 다루는 로봇은 여자유도를 가지기 때문에 위 식에 대한 해는 무한하게 많다. 따라서 최적의 입력 값을 만들 수 있는 QP를 해결하는 방법에 대해 정리하면 아래와 같다.
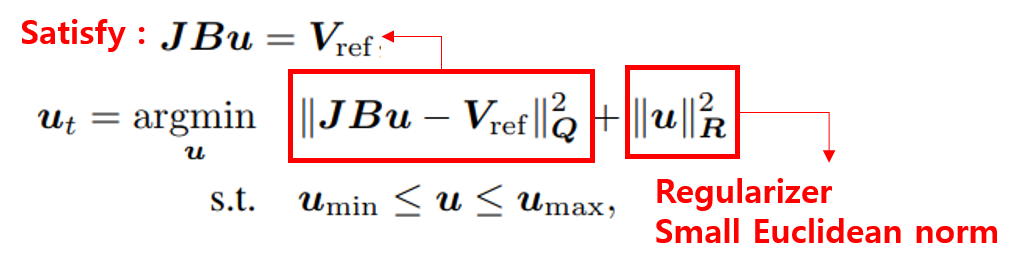
Q와 R은 weight 행렬이다. u_min과 u_max는 조인트 속도의 한계값이 된다. 위의 목적함수에서 첫번째 항은 그 위에 식을 만족하는 형태이며, 두번째 항은 regularizer의 형태로 작용하면서, 작은 유클리디안 norm 값을 갖는 해를 찾도록 해준다.
1. Position and Orientaiton tracking
데카르트 좌표계에서 Desired trajectory에 대한 tracking할 수 있도록 피드백 형태로 twist를 업데이트 해준다.
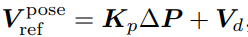
Kp의 경우 게인 행렬이며, EE의 Desired와 current의 차이를 곱하고 desired twist의 feedforward 한다. 한가지 참고해야할 점은 Orientation error를 구하는 방법이다. 이는 아래 식에서 확인할 수 있다.
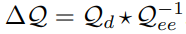
다른 논문에서는 위와 같은 tracking에 있어서 equality constriants의 형태로 QP를 구성하는 방법을 쓰기도 한다. 다만 이번 논문에서는 약간의 flexible을 주어 Desired trajectory에 벗어나도 다른 Safety Constraints를 만족하도록 진행했다.
2. Admittance Control
EE 부분이 스프링 댐퍼 시스템의 형태로 움직이게 하기 위해서 아래와 같은 식을 정의했다.
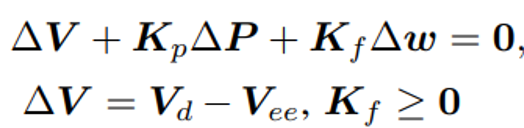
이 식을 만족하기 위해서 EE는 반드시 아래 식을 따라야 한다.
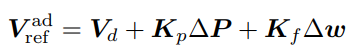
이 식을 잘보면 일반 Desired trajectory tracking식과 비슷한 걸 알 수 있다. 다만 wrench error항이 Kf와 함께 추가 된 걸 확인 할 수 있다. ( 사실 이건 당연한게, 어드미턴스 제어는 위치 기반 임피던스 제어이기 때문에 기존 Tracking에서 약간의 값이 추가된 형태의 값이 나온다.) Kf 값이 0이 되게 되면 Force에 대한 반응이 없고, 반대로 Force에만 반응하는 시스템은 Kp=0인 경우다.
이 외에도 논문에서는 장애물 회피, 밀기, Manipulability에 대해서 이야기를 하는데, 그렇게 중요한 것 같지는 않아서 여기서 마무리 해본다. 실제로 모바일 매니퓰레이터라고 크게 다른 점은 없었고 단순히 아래와 같은 블락 다이어그램을 만들면 되는 것 같다.
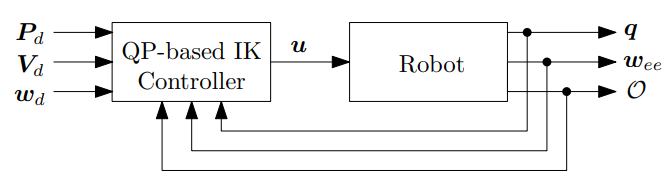
다른 논문들을 조금 더 읽어보고 구현에 들어가봐야겠다.
'미니멀공대생' 카테고리의 다른 글
| 테슬라에서 요구하는 능력을 보자, Tesla Bot (6) | 2023.09.13 |
|---|---|
| 로봇 팔과 카메라 calibration with moveit plugin (0) | 2021.08.10 |
| 강화학습 팁 모음(2) - reward function 작성 요령 (5) | 2021.07.20 |
| 강화학습 팁 모음 (9) | 2021.06.08 |
