티스토리 뷰
Foerster, Jakob, et al. "Counterfactual multi-agent policy gradients." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 32. No. 1. 2018.

0. Comment
MADDPG와 더불어, Centralized learning, Decentralized executing 진영의 대표적인 알고리즘. COMA라 불리고 있으며 discrete action 에 대해서만 다룬다는 것이 MADDPG에 비해 한계점을 가지고 있으나, Deep multi agent reinfrocement learning 관점에서 개별 agent의 공헌도를 부여하는 credit assignment(리워드 할당같은 개념)를 고려했다는 점에서 의미가 있다고 알려진 알고리즘이다. 현재 공식적인 구현체가 존재하지 않아 from scratch로 구현중인데 애먹고있음. 빠뜨린게 없나하는 마음으로 리뷰 시작.
1. Introduction
기존의 강화학습을 통해 single agent의 학습을 진행하는 경우를 보면 많은 발전을 거듭해 왔다. 그러나 다수 로봇 제어나 통신 패킷 전달 같은 다수의 개체를 통제해야하는 경우 single agent 강화학습을 사용하는 방법(예: 스타크래프트에서 한명의 게이머가 여러 유닛을 혼자서 다 조종)을 사용하면 joint action(agent들의 행동 조합) space가 지수적으로 증가하는 문제가 발생한다.
간단하게 2대의 로봇을 통제하는 single agent를 학습시키고 싶은 상황을 생각해보자.
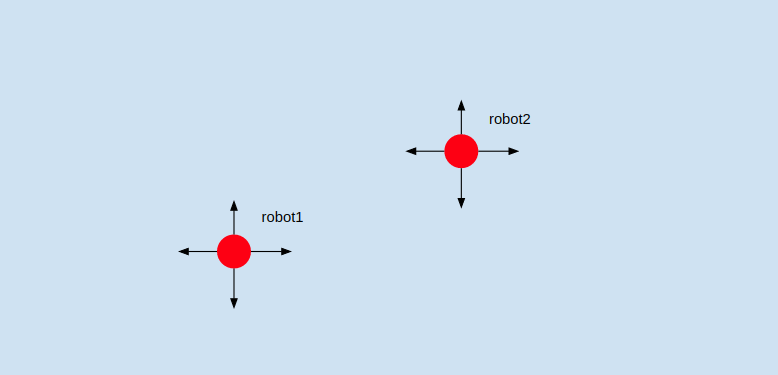
이러면 각 로봇의 action space는 4(상 하 좌 우)이지만, 2대가 되는 순간 single agent가 고려해야할 action space는 $4^2=16$이 된다. (예: (robot1:up, robot2:up), (robot1:up, robot2:right), ....) 이에 따라 action space의 증가는 각 개체의 숫자(n)과 개체가 취할 수 있는 행동(u)에 대해 $$n^u$$이라는 끔찍한 조합적 복잡도를 가지게 된다. 다시 말하면 스타 프로게이머들은 이런 미친 복잡도의 제어를 해내고 있다는 뜻. 따라서 이런 다개체 제어의 상황의 경우 각 개체의 통제를 담당하는 multi agent들을 만들어 학습시키는 방법도 고려될 수 있다. (주: 이게 해결방법이란 것은아니다. multi agent RL은 연구중인 분야)
1-1. Decentralized policy
multi-agent 시스템의 경우 대개 agent 들이 모든 상황을 인지하는 것이 아닌 각 개체마다의 observation의 한계가 존재하는 상황에서 운용이 된다. 이런 상황을 partially observable하다고 한다. 또한 드론같이 활동 범위가 넓은 경우 서로간의 통신을 통해 제어해야하는 제약이 생기기 때문에 agent가 중앙의 명령없이 자가적으로 판단할 수 있는 decentralized system을 구축하는 것이 효율적이다.
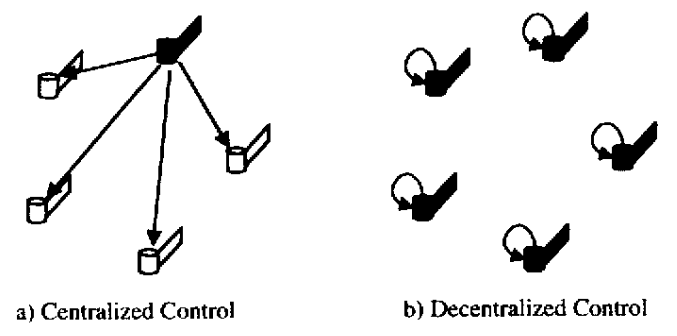
1-2. Central learning, Decentral policy
시뮬레이션을 이용해 강화학습을 하려는 경우, agent가 partially observable하다고 가정하더라도 엔지니어는 사실 전체 상황을 알 수 있다. 이를 이용하여 학습할때만 전체 정보를 활용하는 알고리즘을 사용해 볼 수 있다. 학습자체도 decentral 하게 진행하는 방법도 있겠지만 최대한 많은 정보를 이용한다는 점에서 이점을 노릴 수 있고, 이에 대한 방식은 아직 논란에 있다. (학습도 decentral 하게 하는게 좋다 vs Central 학습 후 decentral 제어가 좋다) 그러나 현재까지는 central-decentral 방식이 MARL(multi agent reinforcement learning)에서 스탠다드로 자리 매김하고 있다. 축구로 따지면 Centralized training of decentralized policies는 대략 이런 느낌.

1-3. Credit assignment
Cooperative task는 대개 전체 agent의 행동 조합에 대한 global reward만을 받을 수 있는 경우가 많다. 이 경우, 각 agent가 global reward에 대해 어느정도 공헌을 하는지 판단하기가 무척 어렵다. 단독 agent에 대한 reward 설정을 미리 해둘 수 도 있지만 서로 협력해야하는 문제의 경우 서로 양보해야(개인 입장에서 더 좋은 reward에 대해) 더 좋은 팀 퍼포먼스가 나오는 경우 같이 굉장히 복잡한 상황에 대해서 다 고려하기가 힘들다. Credit assignment는 MARL에서 주된 연구 분야이기도 하다.
1-4. Contribution of Paper
본 논문은 위에서 거론된 이슈들을 다루기 위해 COMA라는 알고리즘을 제안한다. Actor-Critic을 기본 골자로 하고 있으며, Critic을 이용해 Centralized learning, Actor를 여러개 두어 Decentralized policy를 구현하는 MARL 알고리즘이다. 이 연구는 3가지 contribution을 가지고 있음
- Centralized critic은 오직 학습 중에만 사용된다. Critic은 학습 중 사용가능한 모든 정보(agent들의 action, global state, 각 agent의 observation등)를 받아들여 policy의 학습에 사용된다.
- Counterfactual baseline이라는 개념을 사용하여 credit assignment를 하고자함. Counterfactual baseline은 간단히 말하면 joint action의 global reward에서 내가 알고자하는 agent의 action만을 marginalize시켰다고 보면 된다. 이는 multi agent credit assignment의 개념 중 하나인 difference reward라는 것에서 영감을 얻어 고안했다. 자세히는 본문에서 다룸. COMA는 critic을 이용해 (joint action에 대한 global 기대 return) - (coutnerfactual baseline)을 advantage로써 근사하여 agent policy 업데이트에 사용한다.
- Counterfactual baseline을 계산하는 데 있어서 효율적인 계산 방식을 제안한다. 고안한 Central Critic 구조를 사용하면Global state가 한번의 신경망 통과를 통해 학습 시킬 단독 agent의 모든 action에 대한 Q value를 계산해낸다.
실험환경은 Starcraft에서 진행되었고, 이당시 별달리 비교할 알고리즘이 없어서인지 Actor Critic 알고리즘들과 Central MARL 알고리즘을 비교군으로 사용했다. 결론적으로 Centralized 알고리즘에 비교해 다양한 제약조건을 걸었음에도 비등한 결과가 나온다는 것을 보여준다.
[Related works] 생략
2. Background
2-1. Stochastic game
정의 - $G=<S,U,P,r,Z,O,n,\gamma>$
| S | true state |
| U | joint action |
| P | transition |
| r | global reward |
| Z | each observation |
| O | total observation |
| n | agent number |
| $\gamma$ | discount rate |
이 환경 세팅에서는 agent의 local observation을 고려하기 때문에 $\pi^a(u^a | \tau^{a})$를 사용하여, 이전 모든 step의 trajectory를 고려하여 action을 결정한다.
2-2. Critic 업데이트
본 논문에서는 $TD(\lambda)$방식을 이요하여 critic을 업데이트 한다. Critic function을 $f^c(\cdot,\theta^{c})$ 라 할 때, $TD(\lambda)$ 알고리즘은 다음과같은 mixture n-step return을 사용한다.
$$G^{n}_{t} = \sum\nolimits_{l=1}^{n}\gamma^{l-1}r_{t+l}+\gamma^{n}f^{c}(\cdot_{t+n},\theta^{c})$$
파라미터 $\theta^{c}$는 다음과 같은 loss로 업데이트한다.
$$ \mathbb{L}_{t}=(y^{\lambda}-f^{c}(\cdot_{t},\theta^{c}))^2$$
$$y^{(\lambda)}=(1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t}^{(n)}$$
n-step return인 G의 경우 target-network를 따로 두어 구한다.
3. Method
3-0. Independent Actor-Critic
Baseline으로써 Independent Actor-Critic(IAC)를 고안하여 사용함. IAC는 하나의 critic과 actor신경망 만을 이용하여 agent들이 이 파라미터를 공유하면서 학습하는 형식이다. Partially observable한 환경 때문에 agent들은 같은 신경망을 사용해서 다른 action을 선택함. 업데이트는 일단 actor critic과 같이한다. COMA의 장점 부각에는 사용되나 COMA 알고리즘의 설명에 그닥 중요하진 않음.
3-1. Counterfactual Multi-Agent Policy Gradients
COMA의 가장 큰 key idea는 Couterfactual baseline이다. 이 개념은 Difference Reward[2]에서 영감을 얻었다. Difference reward$D^{a}$는 각 agent가 global reward에 대해 어느정도 공헌도를 가지고 있는지 표현한 reward 식이다.
$$D^{a}=r(s, \mathbf{u})-r\left(s,\left(\mathbf{u}^{-a}, c^{a}\right)\right)$$
$u$는 agent들의 joint action을 나타내고, $u^{-a}$는 agent (a)를 제외한 나머지 agent들의 joint action을 뜻한다. c^{a}는 agent의 default action을 의미하는데, defualt action이란 agent의 policy에 independent한 행동을 의미한다. 이렇게 되면 agent a가 $D^{a}$를 향상시킨다는 것은 global reward인 r(s,a)도 상승시킨다는 말도 된다. 이를 통해 agent a에 대한 credit assignment를 할 수 있게 되는데 몇가지 문제가 발생한다.
- $r\left(\mathbf{u}^{-a},c^{a}\right)$을 구하는 것이 힘들다. 만약 simulation을 사용하고 있다면, agent a를 제외한 나머지 agent들의 action에 대한 reward를 구하기 위해선 simulation을 여러개 사용하여 다 돌려봐하는 어려움이 발생한다.
- 이를 해결하기위하여 approximation을 사용하는 방법이 몇가지 제기 되었는데[3][4], 여전히 문제점은 $c^{a}$를 어떻게 정해야하는가에 대한 것이다. 많은 상황에서 default action을 뭘로 해야할 지 에대해 어려움을 겪는다. 특히 actor critic 구조에서는 추가적인 approximation error까지 발생시켜 더 어렵다.
따라서 COMA에서는 centralized critic을 이용해 Q-value를 추정하여 계산을 효율적으로 만들고자 했다. Advantage 계산을 아래처럼 근사해서 사용한다.
$$A^{a}(s, \mathbf{u})=Q(s, \mathbf{u})-\sum_{u^{\prime a}} \pi^{a}\left(u^{\prime a} \mid \tau^{a}\right) Q\left(s,\left(\mathbf{u}^{-a}, u^{\prime a}\right)\right)$$
식 우항의 2번째 텀이 couterfactual baseline이다. 이런 계산을 deep neural network로 하기 위해선 구조를 좀 신경 쓸 필요가 있는데,
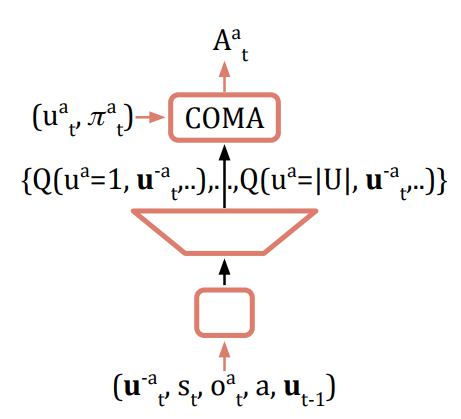
이런 식을 신경망을 설계하면 알고자하는 agent의 각 action에대한 Q value를 다른 agent들의 actoin들을 고정시킨 채로 구할 수 있다. 입력값에 사용되는 튜플은 각각 $u^{-a}$: other agent's actions, $s_t$: global state, $o_t$: observation, $a$: agent type, $u_{t-1}$: previous joint action이다. 실제로 이렇게 다 사용하는지는 알 수 없으나, 적어도 global state와 other agent's action정도는 사용하지 않을까 싶다.
COMA의 agent의 구조는 아래와 같다.

Partial observable 상황을 가정했기에 GRU같은 RNN계열의 층을 사용해서 이전 history를 활용한다. 이런 방식은 Partially observable reinforcement learning연구들을 찾아보면 흔히 등장한다. 여기서 $\epsilon$은 나중에 설명하겠지만 exploration을 위한 계수이다. 이 actor와 critic들을 이용한 COMA의 전체적인 그림은 다음과 같다.

전체적인 학습알고리즘은 논문의 appendix를 확인하면 잘 알 수 있다.
experiment나 결과도 논문 참고하면 될듯.
4. Discussion
COMA알고리즘의 가장 중요한 부분은 credit assignment를 고려했다는 것이다. 성능적인 면이나 세부적인 알고리즘의 경우 그렇게 주목할 만한 것 같지는 않다. 몇가지 한계점이 보였는데
- agent간 정보교환을 전혀 고려하지 않는다. 정해진 시나리오에 대해서는 학습을 잘 할 수 있을 지라도 좀만 동적으로 바뀐 환경이라던가 학습하지 않은 환경에 대한 일반화가 어려울 듯하다.
- scalability에 대한 문제
그래도 agent들에게 각자 credit을 어떻게 할당할 것인지 에대한 노력이 보였다. 현재 구현중인데 TD라던가 이것저것 붙은 알고리즘이라 single agent에 비해 확실히 복잡한 느낌을 받고 있다.
Ref
[1]: Russell Carpenter, J. "Decentralized control of satellite formations." International Journal of Robust and Nonlinear Control: IFAC‐Affiliated Journal 12.2‐3 (2002): 141-161.
[2]: Wolpert, David H., and Kagan Tumer. "Optimal payoff functions for members of collectives." Modeling complexity in economic and social systems. 2002. 355-369.
