티스토리 뷰

최근 Task allocation, Travelling sales man problem, vehicle routing problem과 관련된 연구를 위해 논문을 조사 중인데, 위 문제들은 대체로 combinatorial optimization문제로 귀결된다. NP hard인 이 문제를 학습으로 접근하여 풀려고 했는데 관련 논문들에서 pointer networks가 자주 언급되어 직접 읽기로함. 참고로 위 문제들을 간단히 설명하자면 주어진 task나 way point들에 대해 최적의 루트나 할당 시퀀스를 생성해 주는 문제입니다.
Combinatorial Optimization
input = $P=\left \{ P_1, ..., P_n \right \}$ ex) 방문지역, 할당해야할 임무, 2D point
output = $C^{P}=\left \{ C_1, ..., C_{m(P)} \right \}$ ex) input에 대한 index
위 변환을 원하는 objective나 cost에 대하여 최적화 시켜주는 작업을 combinatorial optimization이라 합니다.

Contribution
- 가변적(variable) 입력에 의존적인 출력 차원 조절
- Convex hull, Delaunay triangluation, TSP 같은 문제들에 적용하여 검증
- 순수 data driven 방식만으로 NP hard 문제를 작은 범위(?)내에서 대략적인 slover를 구현
논문에서 주장하는 contribution인데 개인적으론 1번이 가장 크다고 봅니다.
그럼 가변적 입력에 의존적인 출력 차원 조절이 무슨 말이냐 하면, 일반적으로 Seq2Seq와 Attention method의 한계를 생각해 봅시다. 이 두 방식 모두 학습시에 정해진 차원에 대한 출력만을 결과로 할 수 있는데, Pointer network를 사용하면, 출력 차원이 입력 set 크기와 같게 만들어 줄 수 있어 이런 태생적, 구조적 한계를 극복하게 해줍니다.
문제의 solution의 차원이 input set의 element 갯수와 같은 크기를 가져야하는 일반적인 combinatorial optimization문제를 생각해보면, 가장 필요한 기능이라고 볼 수 있습니다.
Models
논문에서 Seq2Seq, Attention, Ptr-Net을 각각 수학 모델로 표현하고 비교하고 Ptr-Net가 Attention mechanism에 영감을 얻어 설계됐다고 합니다. 각 학습 모델의 목표는 $(P,C^{P})$에 대해 조건부 확률인 $p(C^{P}|P;\theta)$를 구해내는 것이 목적입니다. Seq2Seq, Attention의 경우 배경지식이 없으면 위 링크들에 들어가시면 자세한 설명이 나와 있습니다.


Ptr-Net의 모델을 보면, attention mechanism에서 attention value를 구하기 전 단계인 attention distribution 까지만을 출력으로 하여 최대 값을 input set의 index로 하여 출력이 input 요소를 가리키도록 구조가 짜여진 것을 볼 수 있습니다.
Motivation and data structure
학습에 사용된 $P, C^{P}$ 학습 데이터 셋은 각 문제들에 대한 exact solution으로 생성한 데이터들로 하고, 본 논문에서는 $P$는 2D 데이터 셋을 사용 했습니다. 관련 데이터셋을 따로 공개한 것이 좋네요.
drive.google.com/drive/folders/0B2fg8yPGn2TCMzBtS0o4Q2RJaEU
PTR_NETS - Google 드라이브
drive.google.com
Empirical result
실험의 경우 위의 데이터셋을 이용해 결과를 비교했습니다. LSTM을 이용한 Seq2Seq구조와, attention mechanism, 그리고 Ptr-Net을 비교했네요. 아래 표는 Convex hull에 대해 n의 크기를 가진 $P$에 대하여 학습하고 다양한 크기의 input set에 대해 테스트한 표입니다.
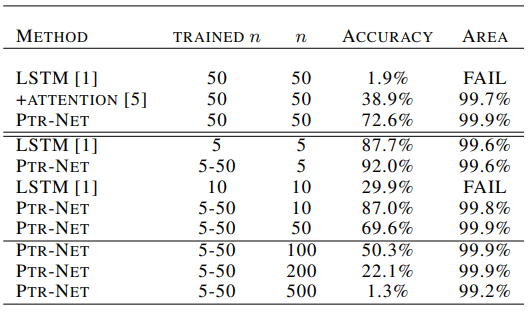
실험구조가 엄청 공평해보이지는 않습니다만 해석을 해보자면, 우선 accuracy는 최적 convex hull과 완전히 일치한 정답을 내놓을 경우를 뜻하고, Area는 최적 convex hull과 겹치는 영역의 비율을 나타낸 것 입니다. FAIL은 제대로된 polygon을 만들어내지 못한 경우를 뜻합니다. PTR-NE의 경우 5-50의 input set크기들에 대해 학습할 경우 500크기의 test set에 대해서도 99.2%의 영역 일치를 보여주는 모습을 보여줍니다. 엄청 scalable 하네요. LSTM(seq2seq)의 경우 FAIL이 자주 뜨는 모습을 볼 수 있는데 FAIL은 아예 결과를 산출하지 못한것이니 치명적이라 보여집니다.
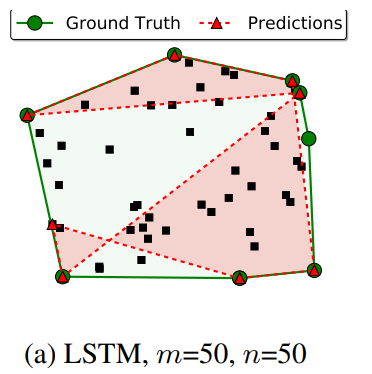
위 그림은 FAIL 사례인데 prediction이 아예 polygon을 형성하지 못한 것을 볼 수 있습니다.

나머지 case(Delaunay triangulation, TSP)에 대해 잘 나온 결과들입니다. TSP의 경우 따로 더 분석한 표를 제공하는데요, NP-hard의 경우라서 더 실험을 진행했다고 보여집니다.

A1, A2, A3는 TSP 문제에 대한 semi optmal한 결과를 만들어내는 알고리즘들의 결과입니다. 각각 $O(n^2)$,$O(n^2)$,$O(n^3)$의 complexity를 보여줍니다. NP-hard문제이니 만큼 Optimal solution은 input set의 크기가 25만 넘어가도 구해내기 힘들어져서 표현 할 수 없게 되고 이 상황에 대한 학습은 A1에서 나온 데이터로 Ptr-NET을 학습시켰다고 합니다. 논문에서는 A1으로 생성한 데이터로 학습 시켰는데도, A1을 outperform하는 점이 흥미로웠다고 합니다.
결과 해석중 몇 가지 걸리는 점은 가끔 Ptr-NET이 invalid output을 결과로 내놓았다는 점인데, 이는 TSP문제에 대해 꽤 치명적이지않나 생각됩니다. 그리고, Convex hull 문제에서 보여지는 scalability도 거의 없다는 한계도 존재하네요.
Discussion
오랜만에 가벼운 마음으로 읽을 수 있었던 논문입니다. 공식적인 구현체가 존재하지 않아 아쉽네요. 그래도 다른 사람들이 구현해 놓은 것은 paper with code에서 검색하면 찾을 수 있습니다.paperswithcode.com/paper/pointer-networks
Papers with Code - Pointer Networks
Implemented in 13 code libraries.
paperswithcode.com
다음번에는 실질적인 구현과, 응용된 논문에 대해 알아보려고 계획중입니다.
