Point cloud :: Surface Normal estimation에 대해서

 

 

출처 : mathworks

Point cloud의 경우 실제 표면에 대한 point들의 집합을 말한다고 볼 수 있다. 따라서 Point 들의 집합으로 어떻게 표면을 나타낼 수 있는지가 중요한 요소가 된다. 표면은 작은 평면들의 집합으로 볼 수 있다. 따라서 먼저 Point set들을 평면으로 나타낼 수 있어야하고 이를 위해 중학생때 배웠던 평면방정식을 한번 되짚어보자.

 

http://blog.daum.net/aero2k/62

 

평면 방정식은 점 3개의 위치만 알면 이를 평면식으로 나타낼 수 있다.

점 p1, p2, p3와 크래머의 정리를 이용해서 평면의 법선벡터와 원점과의 거리 d를 확인 할 수 있다.

 

Pointcloud에서는 2가지 방법으로 법선 벡터를 찾을 수 있다.

 

1. point cloud에서 surface meshing 방법을 이용해 surface를 만들고 mesh를 바탕으로 법선벡터를 구한다.

2. point cloud에서 직접 데이터를 근사하여 surface의 법선벡터를 구한다.

 

내가 사용하는 PCL 라이브러리에서는 2번째 방법으로 법선벡터를 구한다.

 

라이브러리에서는 포인트 클라우드에서 법선벡터를 구하는 것을 a least-square plane fitting estimation problem문제라 두고 평면에서의 법선벡터를 구한다. 이는 하나의 점 혹은 query point에서 가장 인접한 점들의 공분산 행렬의 고유값과 고유벡터를 분석하여 구하게 된다. (PCA). 아래 식에서 k는 point p에서 이웃 점들의 개수이다.

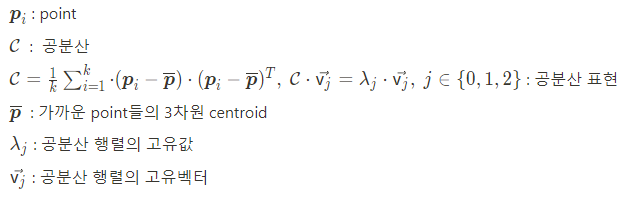
라이브러리내 코드는 아래와 같다.

#include <pcl/point_types.h>
#include <pcl/features/normal_3d.h>

{
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);

  ... read, pass in or create a point cloud ...

  // Create the normal estimation class, and pass the input dataset to it
  pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
  ne.setInputCloud (cloud);

  // Create an empty kdtree representation, and pass it to the normal estimation object.
  // Its content will be filled inside the object, based on the given input dataset (as no other search surface is given).
  pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ> ());
  ne.setSearchMethod (tree);

  // Output datasets
  pcl::PointCloud<pcl::Normal>::Ptr cloud_normals (new pcl::PointCloud<pcl::Normal>);

  // Use all neighbors in a sphere of radius 3cm
  ne.setRadiusSearch (0.03);

  // Compute the features
  ne.compute (*cloud_normals);

  // cloud_normals->size () should have the same size as the input cloud->size ()*

다만, 수학적으로 법선벡터의 부호를 구하는 방법이 없다보니 위에서 설명한 PCA방식으로 법선벡터를 구하는 방식은 약간 애매모호하다. 이로 인해 point cloud 데이터 전부에 대한 법선벡터를 구할 경우 방향이 항상 일정하지만은 않다. 이는 만약 물체를 보고 있는 센서 방향을 알고 있다면 법선벡터의 방향을 센서 방향으로 보게 하려면 아래 식을 만족해야 한다.

 

.

 

방향성 미정

viewpoint에 맞춘 법선벡터

이는 아래 한줄로 해결이 가능하다.

flipNormalTowardsViewpoint (const PointT &point, float vp_x, float vp_y, float vp_z, Eigen::Vector4f &normal);

 

아쉽게도 python-pcl 깃허브에도 normal vector에 대한 부분은 없다.

다만, python에도 PCA에 관한 라이브러리, Scipy 라이브러리에 있는 least-square 등을 활용해서 normal vector를 구할 수 있을 것 같다.

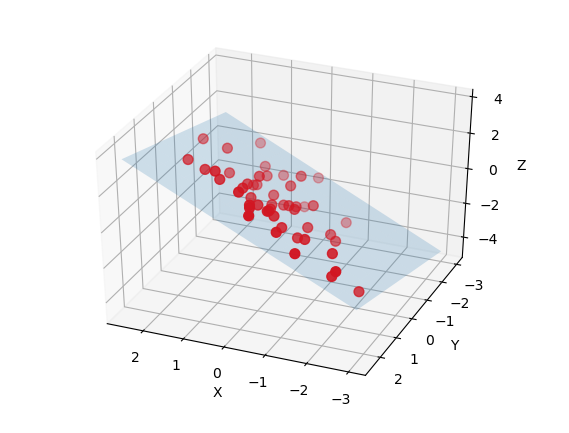
이런식의 point들에 plane를 fitting 시키는 것을 해봤기 때문에, 이런 방식과 KD-tree, knn등을 참고해서

해보면 될 것 같다.

 

 

참고자료

- https://www2.slideshare.net/PirouzNourian/tu-delft-geo1004-2015-point-cloud-processing-estimating-normal-vectors-and-curvature-indicators-using-eigenvectors?from_action=save

- https://github.com/strawlab/python-pcl/tree/master/examples

- https://ko.wikipedia.org/wiki/%EC%B5%9C%EA%B7%BC%EC%A0%91_%EC%9D%B4%EC%9B%83_%ED%83%90%EC%83%89

- https://pointclouds.org/documentation/tutorials/normal_estimation.html