티스토리 뷰
인사
안녕하세요 오랜만의 글입니다. :)
최근에 공부하고 있는 분야는 모바일 로봇의 임무 계획(mission planning)인데, 간단히 말하자면 로봇이 수행할 다수의 작업(task/mission)들이 존재 할 때 이를 어떤 로봇이, 어떤 순서로 수행할 지에 대한 분야입니다. 아직 로보틱스쪽에서는 control, path planning, motion planning처럼 많이 정립되고 교육되고있는 분야는 아니라서 task allocation/assignment/scheduling/planning, mission planning 등등 다양한 용어로 언급되고 있습니다.
저는 임무 계획을 다수의 로봇을 운용하는 경우 임무계획=작업할당 + 작업계획으로 나누어 생각하고 있고, 이를 계층적으로 나눠서 풀거나 한번에 푸는 방법들이 많이 연구되고 있는 것 같습니다.
오늘 포스팅하게 될 내용은 작업할당의 가장 기본적인 알고리즘으로 알려진 Hungarian Algorithm에 대한 내용인데, 로봇의 작업할당을 한다면 어떻게 쓰이는지, 그리고 매우 간단한 코드를 소개하면서 마치도록 하겠습니다. 아무래도 짬을 내서 매우 조금씩 쓰던 포스트라, 두서가 없다는 점은 미리 죄송합니다.
아, 매니퓰레이터의 경우도 많이 다뤄지는 주제이긴 한데,, 이부분은 다음에 다뤄보도록 하겠습니다. 그래서 아래부터 언급되는 로봇은 드론, 모바일 로봇 같은 무인이동체로 생각해주시면 되겠습니다.
작업 할당
로보틱스에서 언제 작업 할당이 요구될까요?
최근 단일 로봇 운용의 안정도가 상승하고, 이에 따라 많은 산업체/기관들이 로봇 개발의 상용화에 뛰어듬에 따라 여러 분야에서 로봇의 도입이 진행되고 있습니다.

특히 배달, 물류, 서빙, 탐사, 교통 같은 분야에서는 운용하기위한 로봇의 대수가 많아질 수 밖에 없고, 이에 따라 각 로봇들에게 어떤 작업을 할당 시킬 것인지를 잘 결정하는 방법들이 많이 요구되고 있습니다.
뭔가 대단한 것을 할 것처럼 서론을 띄웠지만, 오늘 얘기할 주제는 할당 문제(assignment problem)에서 가장 기본적으로 등장하는 헝가리안 알고리즘(Hungarian Algorithm)의 활용에 대해 얘기해 보고자 합니다. 사실 이런 할당문제는 로보틱스가 아니라도 경영과학이나 산업 공학같은 분야에서도 많이 사용되고 있습니다.
기본적인 할당문제는 내가 운용할 로봇들이 주어진 작업들을 수행할 때 필요한 운용 비용(사용 연료, 전체 작업 종료 시간)을 최소화하거나, 얻을 수 있는 이득을 최대화하는 것을 목표로 합니다.
간단한 예시로 아래 표와 같이 로봇이 수행할 작업에 대한 비용(cost)를 표현 할 수 있습니다.
| 로봇\작업 | 작업 1 | 작업 2 | 작업 3 |
| 로봇 1 | 3 | 2 | 1 |
| 로봇 2 | 3 | 4 | 6 |
| 로봇 3 | 7 | 3 | 5 |
이때 각 로봇이 서로 겹치지 않게 작업 작업을 하나씩 선택하여, 전체 드는 비용을 최소화하는 조합을 찾아야 합니다.
가장 간단한 방법을 생각해보면, 모든 할당에 대한 조합을 다 구해놓고 그 중 최소 비용을 지니는 조합을 선택하면 될 것 입니다. 보통 brute force, exhaustive search라고 부릅니다. 이러면 아주 단순하고도 확실하게, 가장 최적의 조합을 선택할 수 있습니다. 그러나 이렇게 되면 주어진 로봇과 작업의 갯수가 $N$ 이라 할 때 탐색 복잡도는 $O(N!)$ 이라는 처참한 결과가 나올 것 입니다.
여기서 좀 더 빠르게 최적으로 할당 문제를 해결 할 수 있게 해주는 알고리즘이 헝가리안 알고리즘 입니다.
기본적인 헝가리안 알고리즘에 대한 설명은 아래 링크의 블로그에서 정말 자세하게 설명해주고 있으니 참고하시면 됩니다.
할당 문제 & 헝가리안 알고리즘 (Assignment Problem & Hungarian Algorithm)
이번 포스팅에서는 assignment problem과 Hungarian algorithm에 대해서 알아보겠습니다. 먼저 assignment problem이 어떤 것인지에 대해서 살펴보고, 이를 해결하는 방법을 알아보도록 하겠습니다. 인터넷을 찾
gazelle-and-cs.tistory.com
모바일 로봇으로 할 수 있는 다양한 작업(visiting, area coverage, loitering, delivery, tracking 등)들이 존재하지만 오늘은 가장 간단한 지역 방문(visiting)에 대한 할당을 다뤄보도록 하겠습니다. 방문 외의 작업들에 대한 cost를 어떻게 결정할 건지 등의 연구도 정말 재미있는 주제입니다.
Visiting 할당 문제의 경우 로봇과 작업 지역사이의 거리를 주로 비용으로 두고 문제를 풀게 됩니다. 즉 할당 알고리즘을 실행하는 시점에서 로봇들의 위치와 작업들의 위치가 주어졌을 때 전체 로봇의 이동거리가 최소가 되도록 할당문제를 풀고자하는 것이 오늘 예제의 목표입니다.
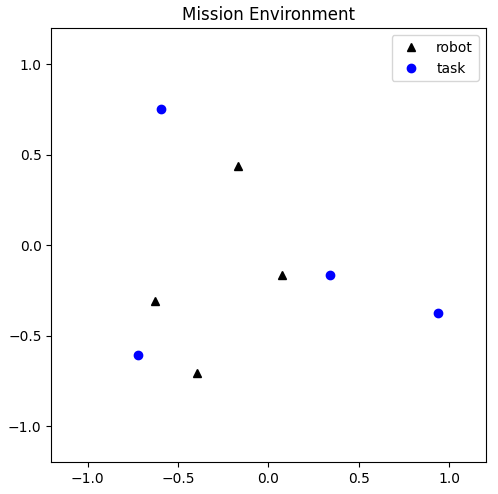
헝가리안 알고리즘의 경우 고맙게도 scipy 라이브러리에서 지원을 해 주고 있습니다.
scipy.optimize.linear_sum_assignment — SciPy v1.8.0 Manual
docs.scipy.org
핵심 코드
np.random.seed(1)
# Number of robots and tasks
n_robot = 4
n_task = 4
# randomly generates the pose of robots and tasks
robot_pos = np.random.uniform(-1,1,size=(n_robot, 2))
task_pos = np.random.uniform(-1,1,size=(n_task, 2))
# calculates a distance matrix as the cost
cost = distance_matrix(robot_pos, task_pos)
# Hungarian algorithm
row_ind, col_ind = linear_sum_assignment(cost)
# cacluates the total cost of the result
total_cost = cost[row_ind, col_ind].sum()결과
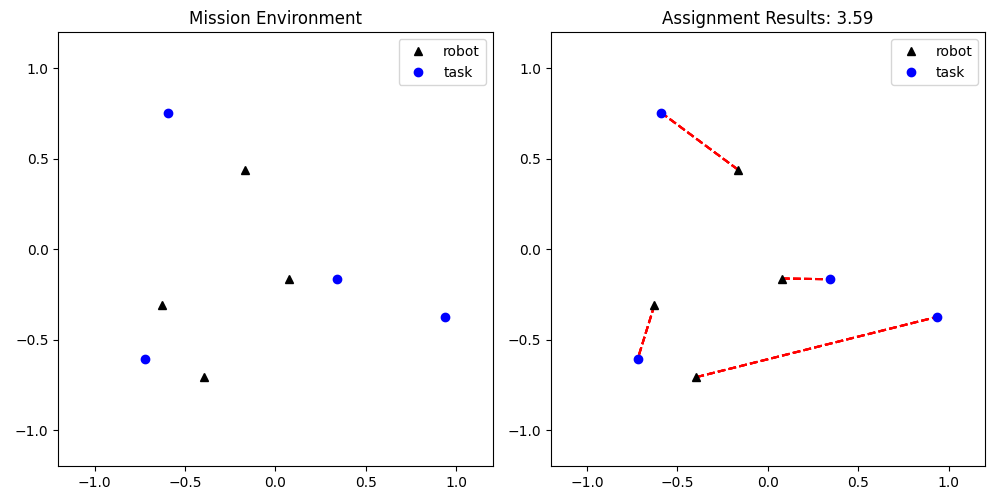
위 그림을 보면 로봇들이 어떤 작업들에 할당 되었는 지 확인이 가능합니다.
여기서 드는 의문은 그냥 각 로봇에 가장 가까운 지역에 할당시켜주면 되는 거 아닌가? 라는 물음이 발생하게 되는데요, 이런 방식을 greedy algorithm이라고 합니다. 이 방식도 문제의 복잡도가 위 상황처럼 낮은경우 나름 괜찮게 작동하는 것을 볼 수 있습니다. 그러나 문제의 스케일이 커지면 커질 수록 뒤에서 나중에 할당될 로봇의 결과를 생각하지 않기 때문에 비효율적인 할당들이 일어나게 됩니다.
Greedy Algorithm과의 비교 (robot:10, task:10)
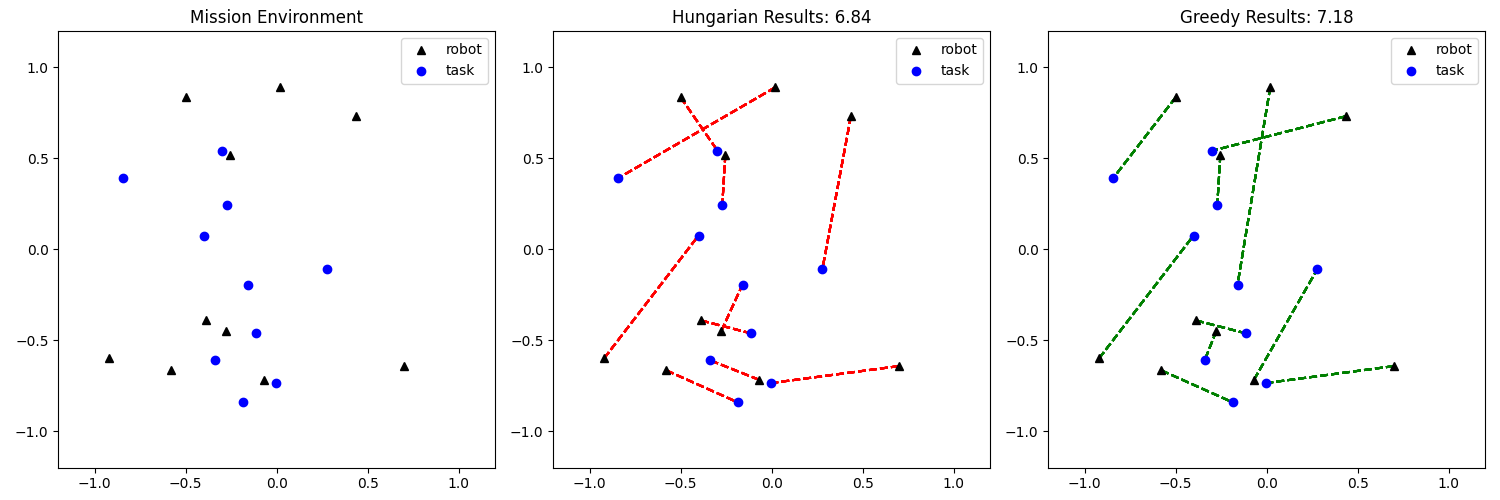
위 그림에 보이시는 것처럼 Hungarian Algorithm은 항상 최적을 만족하기 때문에 Greedy 알고리즘보다 더 좋은 성능을 보이는 것을 확인할 수 있습니다.
전체 코드
import numpy as np
from scipy.spatial import distance_matrix
from scipy.optimize import linear_sum_assignment
from matplotlib import pyplot as plt
np.random.seed(15)
# Number of robots and tasks
n_robot = 10
n_task = 10
# randomly generates the pose of robots and tasks
robot_pos = np.random.uniform(-1,1,size=(n_robot, 3))
task_pos = np.random.uniform(-1,1,size=(n_task, 3))
# Create figure
fig, ax = plt.subplots(1,3,figsize=(15,5))
# plot initial mission environment
ax[0].plot(robot_pos[:,0], robot_pos[:,1], 'k^',label="robot")
ax[0].plot(task_pos[:,0], task_pos[:,1], 'bo', label="task")
ax[0].set_title("Mission Environment")
ax[0].set(xlim=(-1.2,1.2),ylim=(-1.2,1.2))
ax[0].set_aspect("equal")
ax[0].legend()
# calculates a distance matrix as the cost
cost = distance_matrix(robot_pos, task_pos)
# Hungarian algorithm
row_ind, col_ind = linear_sum_assignment(cost)
# cacluates the total cost of the result
hungarian_total_cost = cost[row_ind, col_ind].sum()
print("Hungarian Result: {}".format(col_ind))
print("Hungarian Cost: {:.3}".format(hungarian_total_cost))
# plot Hungarian assignments
for i in range(len(col_ind)):
ax[1].plot([robot_pos[row_ind,0],task_pos[col_ind,0]],[robot_pos[row_ind,1],task_pos[col_ind,1]],'r--')
ax[1].plot(robot_pos[:,0], robot_pos[:,1], 'k^',label="robot")
ax[1].plot(task_pos[:,0], task_pos[:,1], 'bo', label="task")
ax[1].set_title("Hungarian Results: {:.3}".format(hungarian_total_cost))
ax[1].set(xlim=(-1.2,1.2),ylim=(-1.2,1.2))
ax[1].set_aspect("equal")
ax[1].legend()
# greedy algorithm
greedy_task = []
greedy_total_cost = 0
for robot in range(n_robot):
cand_task = list(np.argsort(cost[robot, :]))
while True:
task = cand_task[0]
if task not in greedy_task:
greedy_task.append(task)
greedy_total_cost += cost[robot, task]
break
else:
cand_task.pop(0)
greedy_task = np.array(greedy_task)
print("Greedy Result: {}".format(greedy_task))
print("Greedy Cost: {:.3}".format(greedy_total_cost))
# plot Greedy assignments
for i in range(len(col_ind)):
ax[2].plot([robot_pos[row_ind,0],task_pos[greedy_task,0]],[robot_pos[row_ind,1],task_pos[greedy_task,1]],'g--')
ax[2].plot(robot_pos[:,0], robot_pos[:,1], 'k^',label="robot")
ax[2].plot(task_pos[:,0], task_pos[:,1], 'bo', label="task")
ax[2].set_title("Greedy Results: {:.3}".format(greedy_total_cost))
ax[2].set(xlim=(-1.2,1.2),ylim=(-1.2,1.2))
ax[2].set_aspect("equal")
ax[2].legend()
fig.tight_layout()
plt.show()마무리
오늘은 헝가리안 알고리즘의 매우 간단한 활용에 대한 이야기를 했습니다. 사실 로봇이라는 용어를 굳이 끌고 오지 않아도 설명이 가능한 내용이긴 하지만, 생각 보다 많은 멀티로봇 연구들에서 아직 사용되고 있고 로봇을 대입하면 대강 어떤 cost를 사용하는지도 언급을 하고 싶었습니다.
또한, 오늘 언급을 안한 내용들이 있는데, 로봇이나 작업이 더 많은 상황은 어떻게 할 것인지, 단순한 지역방문이 아니라 추적이나 패트롤같은 지속적인 작업들에 대해서는 어떻게 처리할지에 대한 상황들도 생각해볼 거리입니다. 그리고 현실적인 운용을 생각했을 때 단발적인 방문 문제라 하더라도 할당된 지역의 방문을 먼저 수행한 로봇이 아직 처리되지 않는 지역을 추가적으로 방문하는 planning 관점에서의 생각도 해 볼 수 있고, 여러모로 많은 생각을 하게하는 주제들이 무궁무진하게 펼쳐져 있습니다.
앞으로도 이런 줄기의 내용들에 대해서도 시간 나면 풀어보도록 하겠습니다.
'keep9oing' 카테고리의 다른 글
| [논문리뷰]Sold!: Auction methods for multirobot coordination (0) | 2022.11.21 |
|---|---|
| Robotarium - 원격 로봇 테스트 베드 (5) | 2022.04.07 |
| Evolutionary strategy 2 - Elitarian selection evolution (2) | 2021.07.18 |
| Evolutionary strategy 1 - Simple Gaussian Evolution (7) | 2021.07.16 |
| Graph spectral partitioning/clustering with python (0) | 2021.05.13 |
